Linear Models

Kacper Sokol

Model Overview

Model Synopsis


A linear model predicts the target as a weighted sum of the input features.


The independence and additivity of the model’s structure make it transparent. The weights communicate the global (with respect to the entire model) feature influence and importance.

Toy Example


\[ f(\mathbf{x}) = -1.81 \;\; + \;\; 0.54 \times x_1 \;\; + \;\; 0.34 \times x_2 \]


\[\omega_0 = -1.81 \;\;\;\;\;\;\;\; \omega_1 = 0.54 \;\;\;\;\;\;\;\; \omega_2 = 0.34\]

Toy Example    

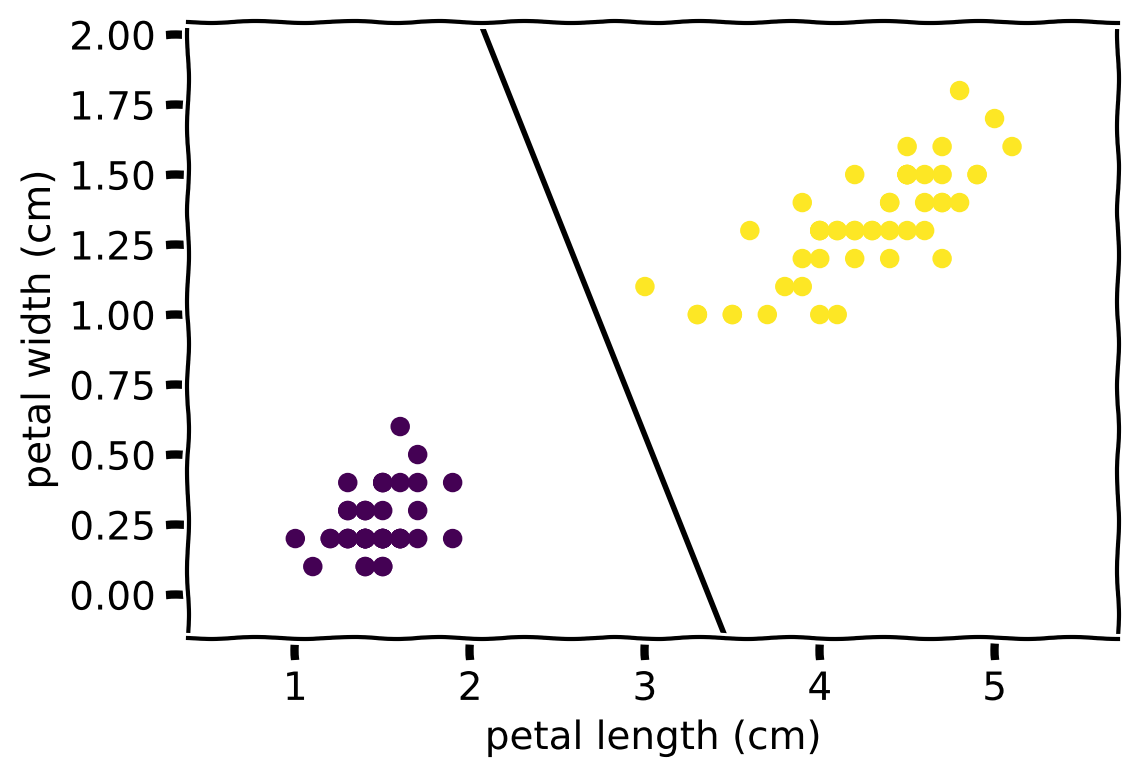
Linear model for 2 features

Explanation Properties


Property Linear Models
relation ante-hoc
compatibility linear models
modelling regression (crisp classification)
scope global and local
target model and prediction

Explanation Properties    


Property Linear Models
data tabular
features numerical and (one hot-encoded) categorical
explanation model visualisation, feature influence & importance
caveats feature correlation, target nonlinearity

Examples

Model Visualisation

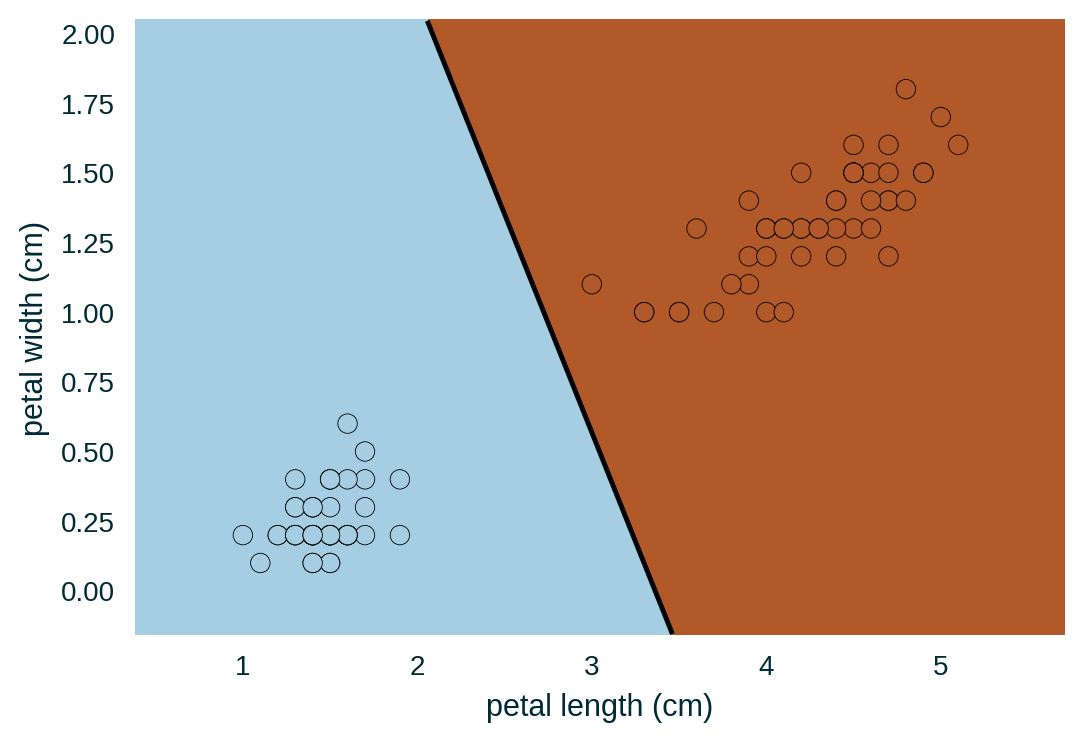
Linear model for 2 features

Model Equation


\[ f(\mathbf{x}) = -1.81 \;\; + \;\; 0.54 \times x_1 \;\; + \;\; 0.34 \times x_2 \]


\[\omega_0 = -1.81 \;\;\;\;\;\;\;\; \omega_1 = 0.54 \;\;\;\;\;\;\;\; \omega_2 = 0.34\]

Feature Influence & Importance

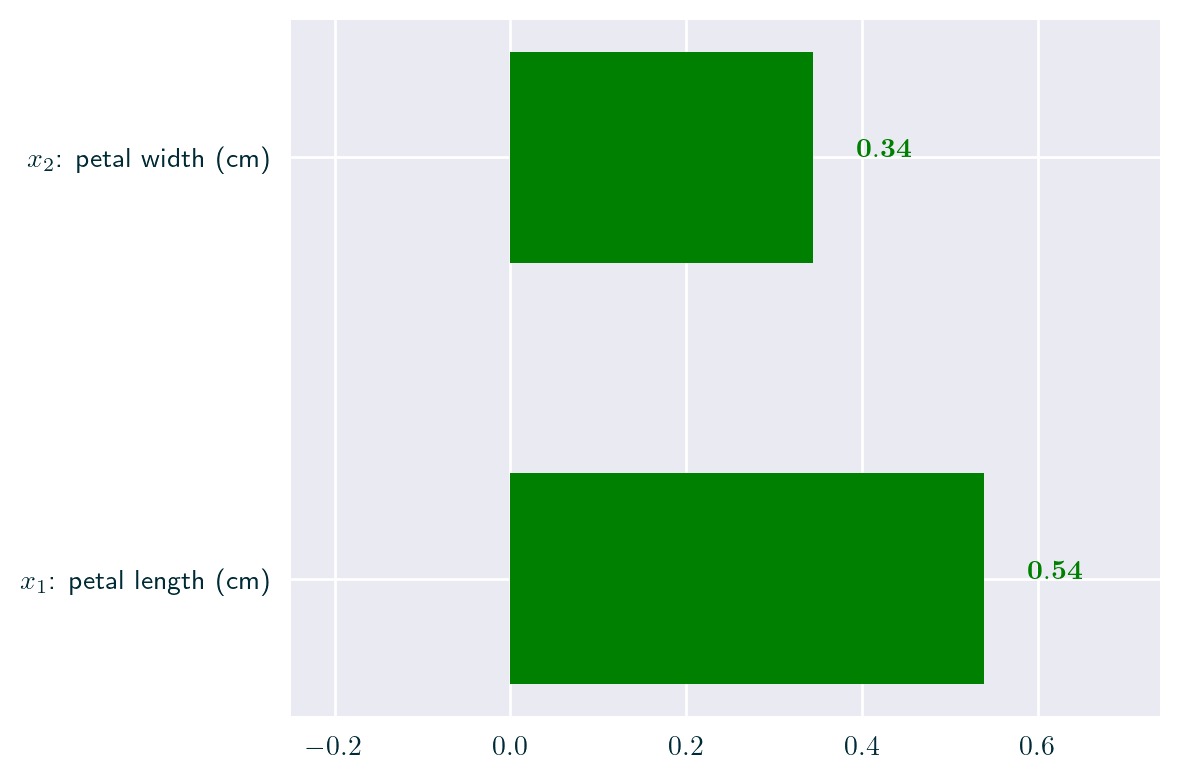
Bar plot explanation

Feature Effect

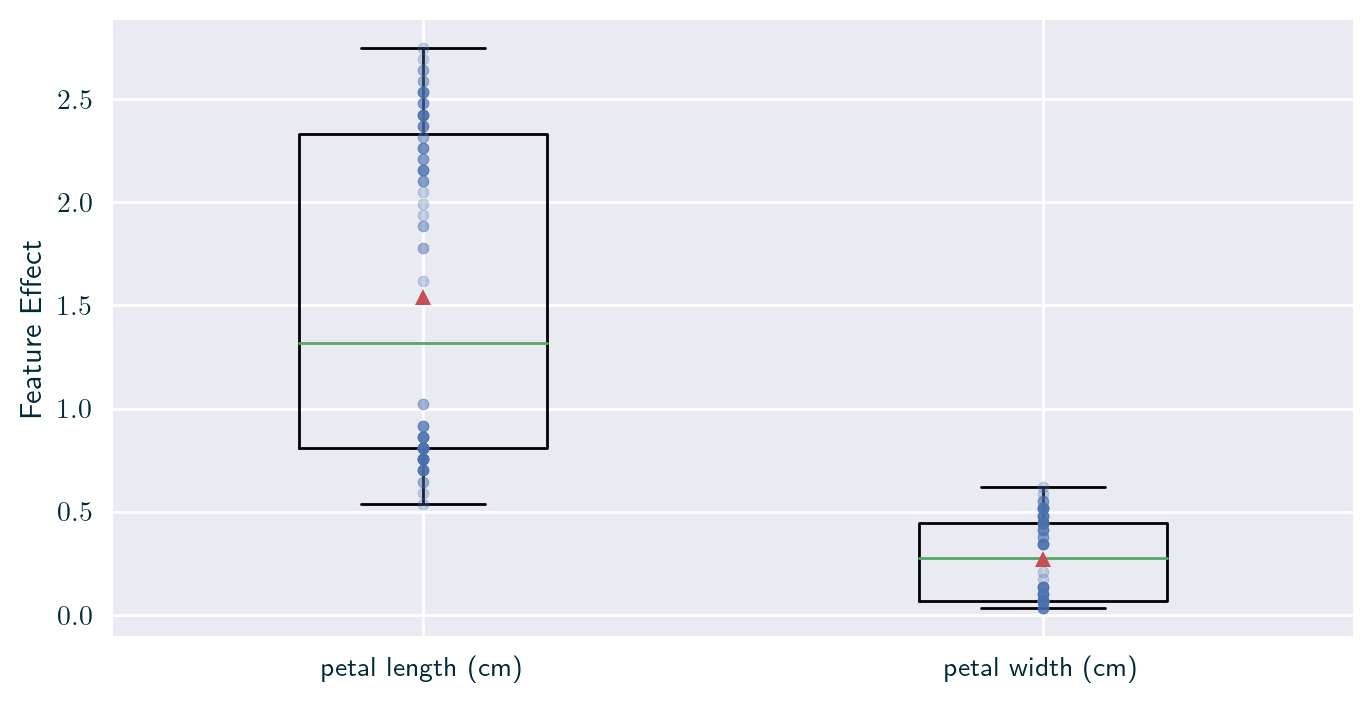
Feature effect -- box plot

Feature Effect    

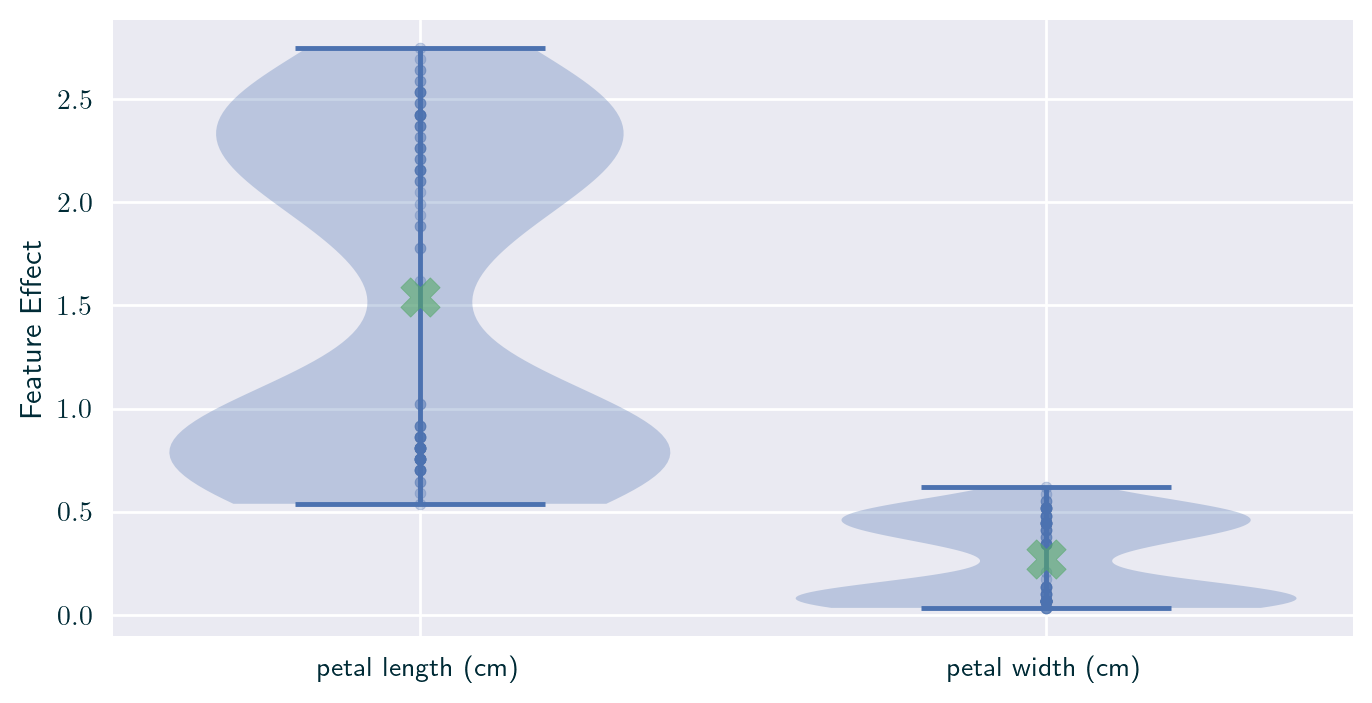
Feature effect -- violin plot

Individual Effect

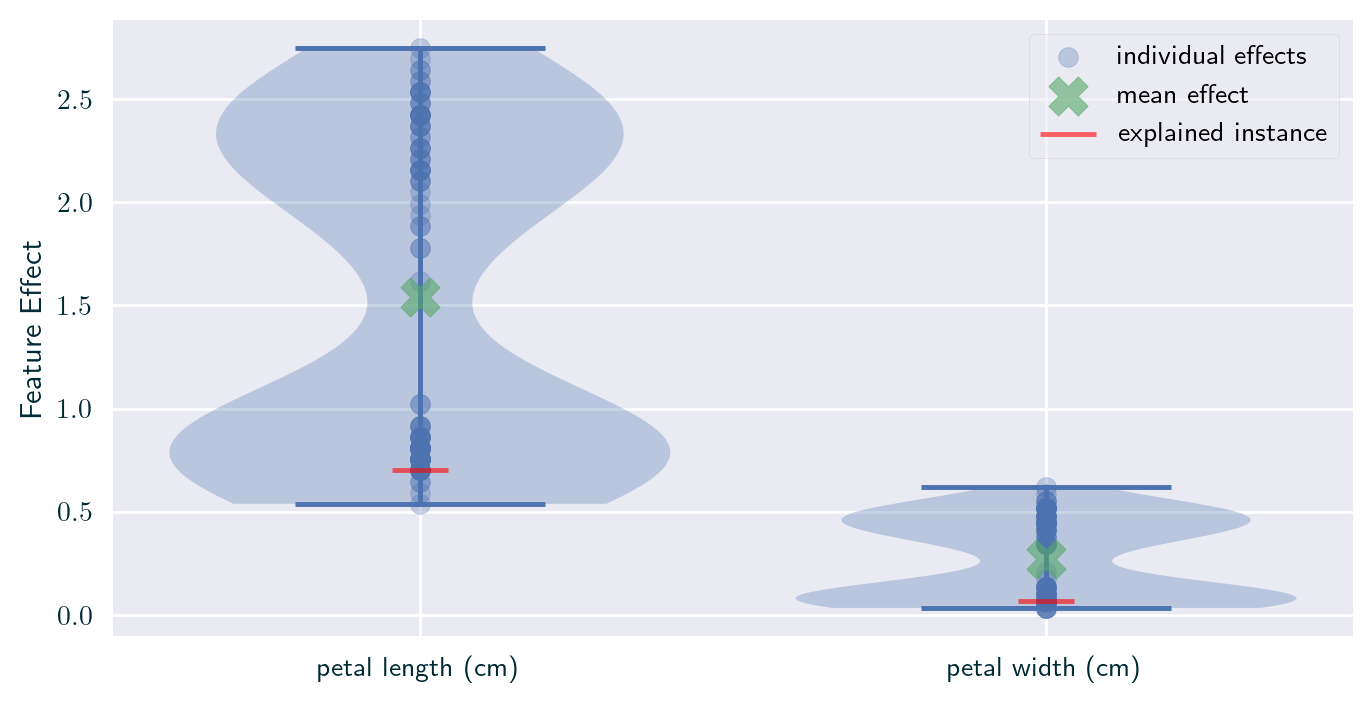
Individual effect -- violin plot

Individual Effect    


\[\omega_0 = -1.81 \;\;\;\;\;\;\;\; \omega_1 = 0.54 \;\;\;\;\;\;\;\; \omega_2 = 0.34\]


\[x_1 = 1.30 \;\;\;\;\;\;\;\; x_2 = 0.20\]

Individual Effect    


\[ f(\mathbf{x}) = -1.81 \;\; + \;\; \underbrace{0.54 \times 1.30}_{x_1} \;\; + \;\; \underbrace{0.34 \times 0.20}_{x_2} \]


\[ f(\mathbf{x}) = -1.81 \;\; + \;\; \underbrace{0.70}_{x_1} \;\; + \;\; \underbrace{0.07}_{x_2} \]

Individual Effect    

Visualization omitted, Javascript library not loaded!
Have you run `initjs()` in this notebook? If this notebook was from another user you must also trust this notebook (File -> Trust notebook). If you are viewing this notebook on github the Javascript has been stripped for security. If you are using JupyterLab this error is because a JupyterLab extension has not yet been written.

Textualisation


Increasing petal length (cm) by 1, increases the prediction by 0.54, ceteris paribus.

Increasing petal width (cm) by 1, increases the prediction by 0.34, ceteris paribus.

Variants

Feature Interaction


Manually introducing feature interaction terms allows linear models to account for such phenomena.


\[ f(\mathbf{x}) = \omega_0 + \omega_1 x_1 + \cdots + \omega_n x_n + \underbrace{\omega_{n+1} x_4 x_6}_{\textit{interaction}} \]

Generalized Linear Models


Generalized Linear Models (GLMs) allow to model alternative (to Gaussian) distributions of the prediction target.


\[ g(\mathbb{E}_Y(y|\mathbf{x})) = \omega_0 + \omega_1 x_1 + \cdots + \omega_n x_n \]

Generalized Additive Models


Generalized Additive Models (GAMs) allow to model nonlinear relationships – a weighted sum is replaced by a sum of arbitrary functions.


\[ g(\mathbb{E}_Y(y|\mathbf{x})) = \omega_0 + f_1(x_1) + \cdots + f_n(x_n) \]

Many More


This list is far from comprehensive and exhaustive.

Case Studies & Gotchas!

Feature Selection


  • Large models may become overwhelming and incomprehensible (but still transparent)
  • Achieved with feature selection or sparse linear models


\[ f(\mathbf{x}) = 0.2 \;\; + \;\; 0.25 \times x_1 \;\; - \;\; 0.47 \times x_2 \;\; + \;\; 0.01 \times x_3 \;\; + \;\; 0.70 \times x_4 \\ - \;\; 0.20 \times x_5 \;\; - \;\; 0.33 \times x_6 \;\; - \;\; 0.90 \times x_7 \]

Incomparability of Parameters

  • The coefficients are uninformative unless the features are standardised (zero mean, one standard deviation) \[ \mathring{x}_i = \frac{x_i - \mu_i}{\sigma_i} \]
  • The reference point becomes an all-zero instance – a mean-valued data point
  • The intercept communicates the prediction of the reference point

Feasibility of the Reference Instance

The reference point may be out-of-distribution.

Incomparability of Parameters    

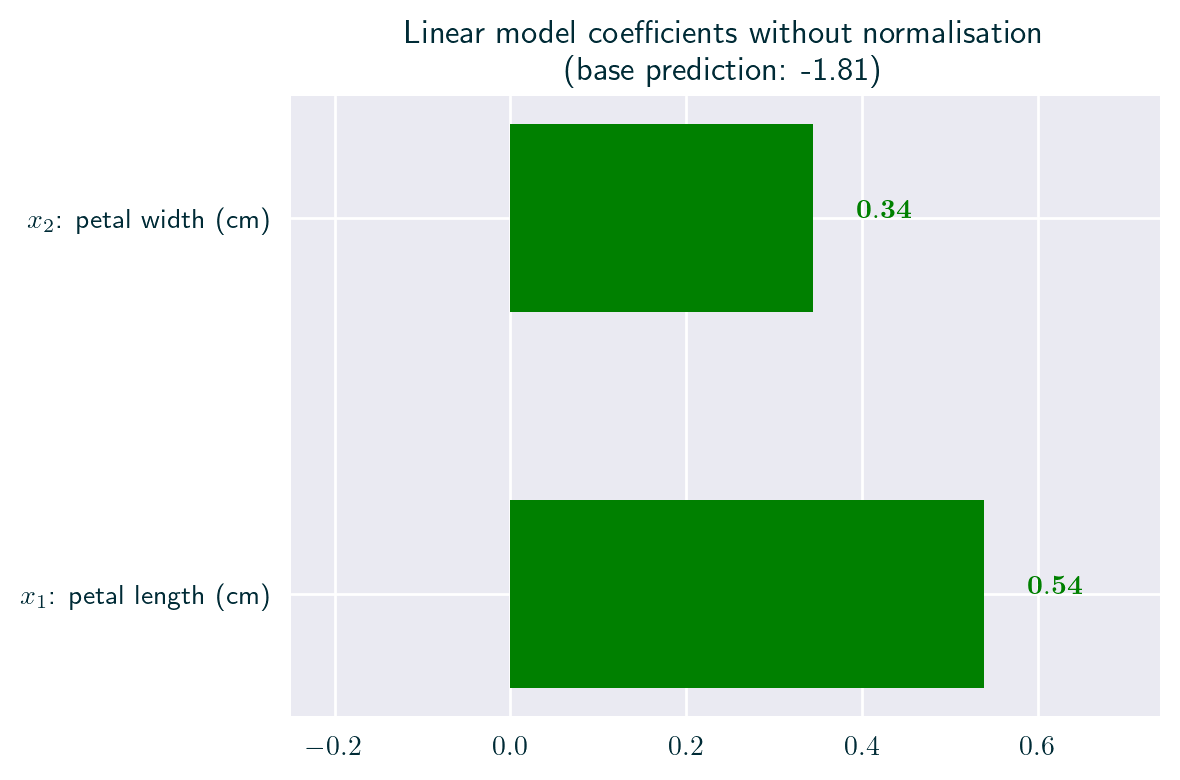
Bar plot explanation -- no normalisation

Incomparability of Parameters    

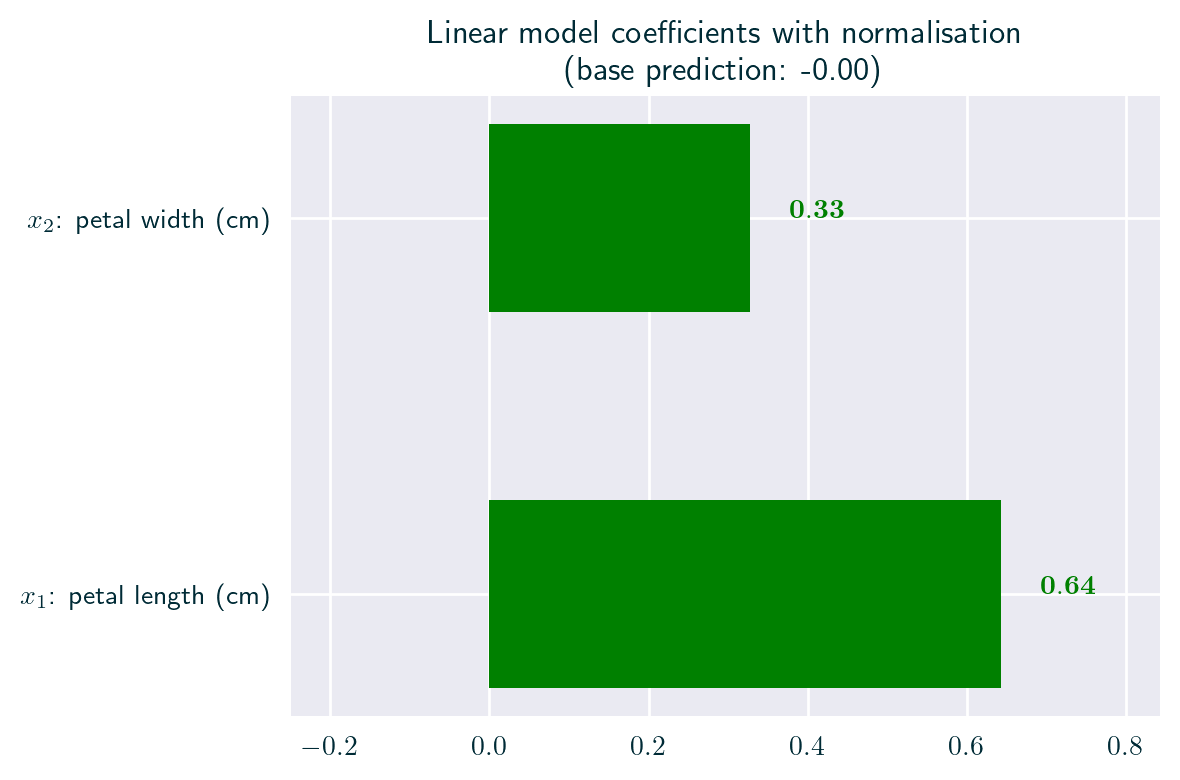
Bar plot explanation -- normalisation

Incomparability of Parameters    

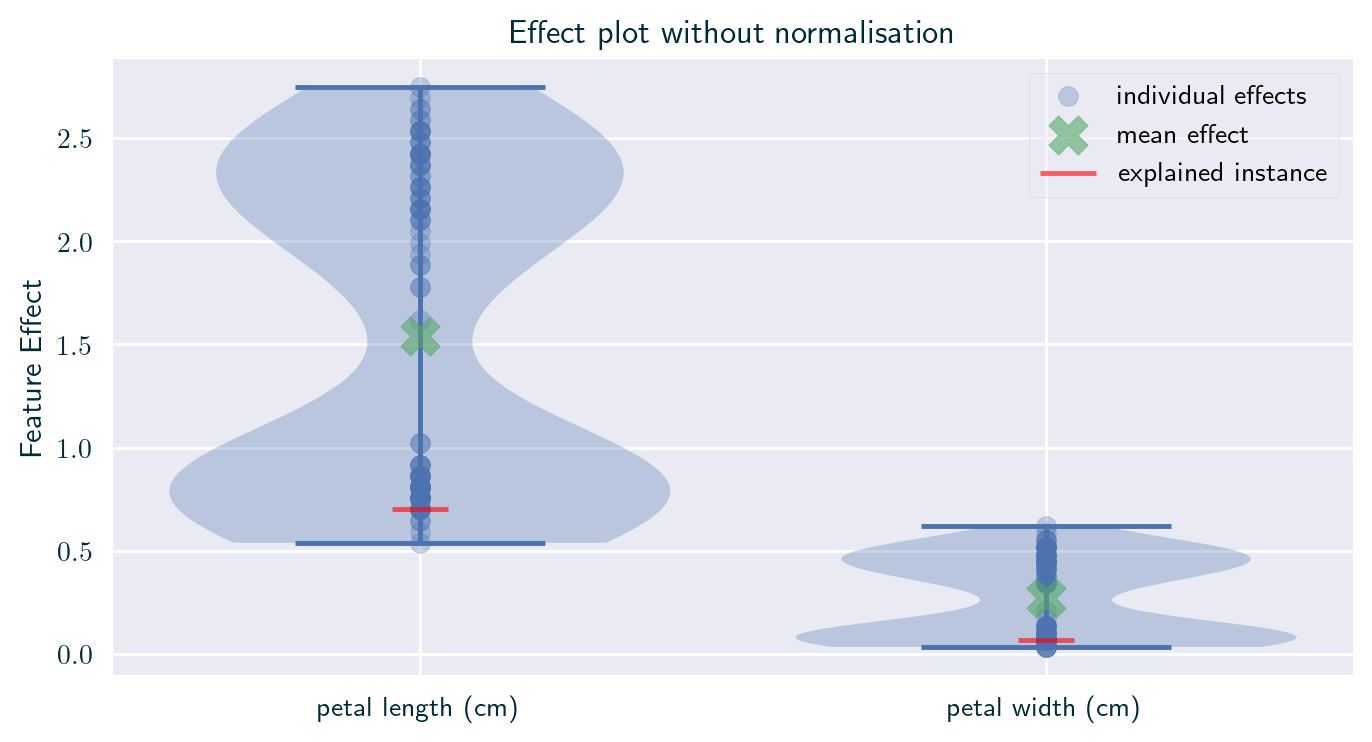
Individual effect without normalisation -- violin plot

Incomparability of Parameters    

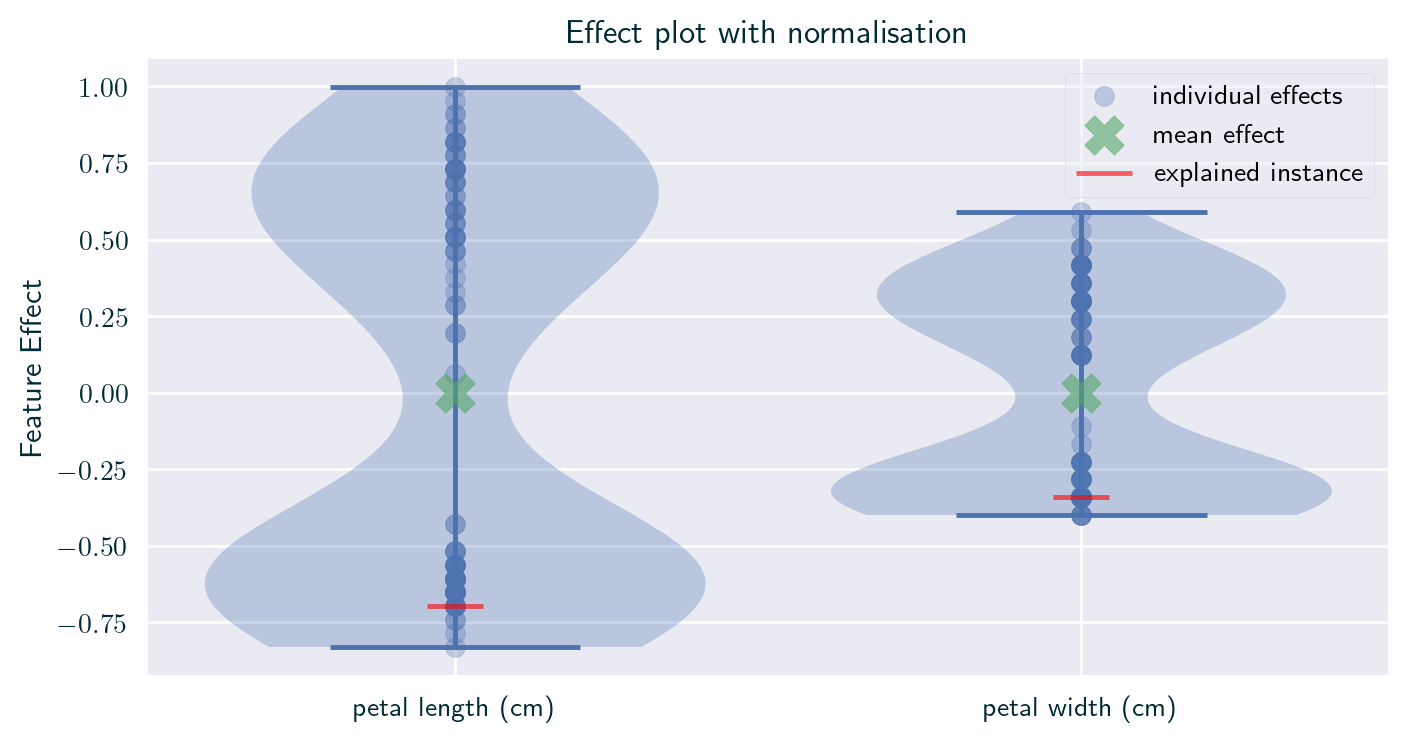
Individual effect with normalisation -- violin plot

Incomparability of Parameters    

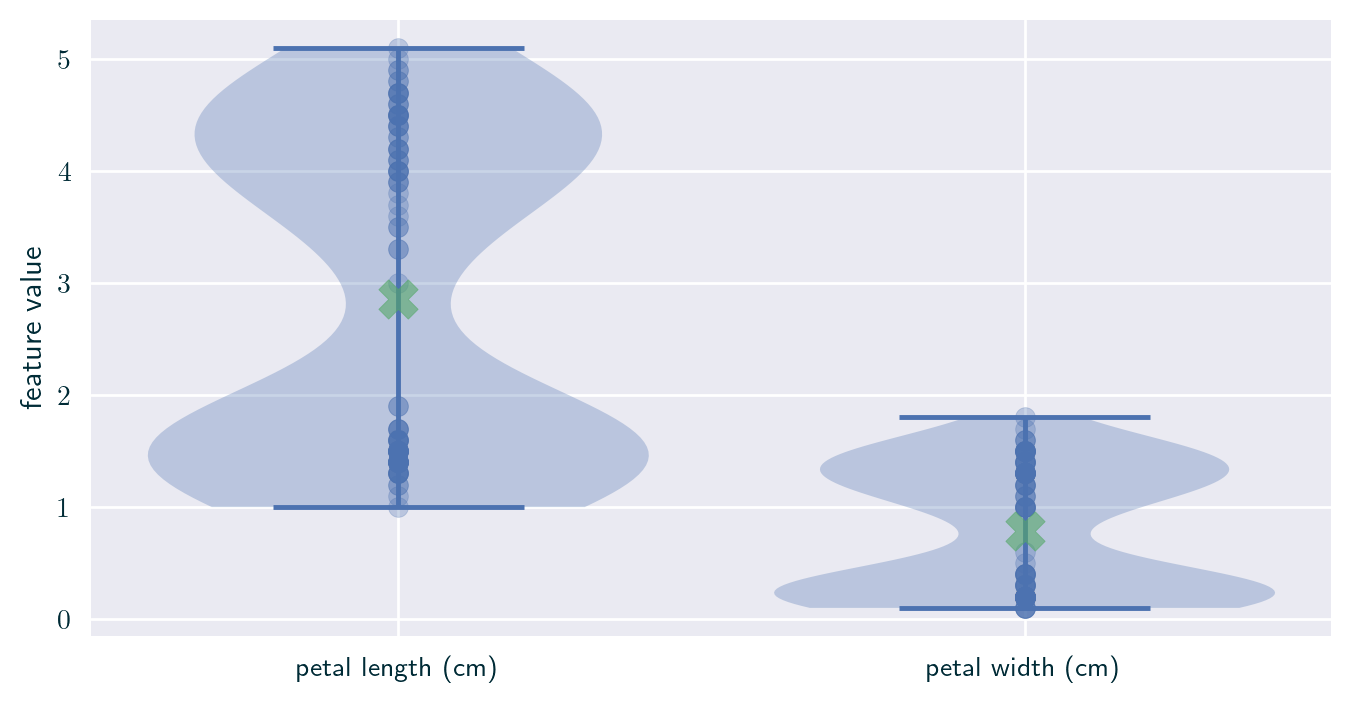
Feature value distribution

Properties

Pros    

  • Transparent from the outset due to linearity – predictions are a linear combination of features
  • Easy to interpret (given relevant background knowledge)

Cons    

  • Model linearity entails low complexity, but also low expressivity, hence low predictive power
  • Feature interactions / correlations are not accounted for
  • Poor modeling ability for nonlinear problems
  • Decreased transparency for a large number of features (can be overcome with feature selection)

Caveats    

  • Interpretability is tricky without feature normalisation
  • The interpretation based on unitary change in feature values ignores feature correlation and may lead to out-of-distribution instances

Further Considerations

Summary

  • (Small) linear models are transparent
  • Their interpretation should be viewed through their inherent limitations

Implementations

Python R
scikit-learn built in

Further Reading

Bibliography

Flach, Peter. 2012. Machine Learning: The Art and Science of Algorithms That Make Sense of Data. Cambridge university press.
Nelder, John Ashworth, and Robert WM Wedderburn. 1972. “Generalized Linear Models.” Journal of the Royal Statistical Society: Series A (General) 135 (3): 370–84.

Questions