Permutation Feature Importance (PFI)
/Model Reliance/
(Feature Importance)
Method Overview
Explanation Synopsis
PFI – sometimes called Model Reliance (Fisher, Rudin, and Dominici 2019) – quantifies importance of a feature by measuring the change in predictive error incurred when permuting its values for a collection of instances (Breiman 2001).
It communicates global (with respect to the entire explained model) feature importance.
Rationale
PFI was originally introduced for Random Forests (Breiman 2001) and later generalised to a model-agnostic technique under the name of Model Reliance (Fisher, Rudin, and Dominici 2019).
Toy Example
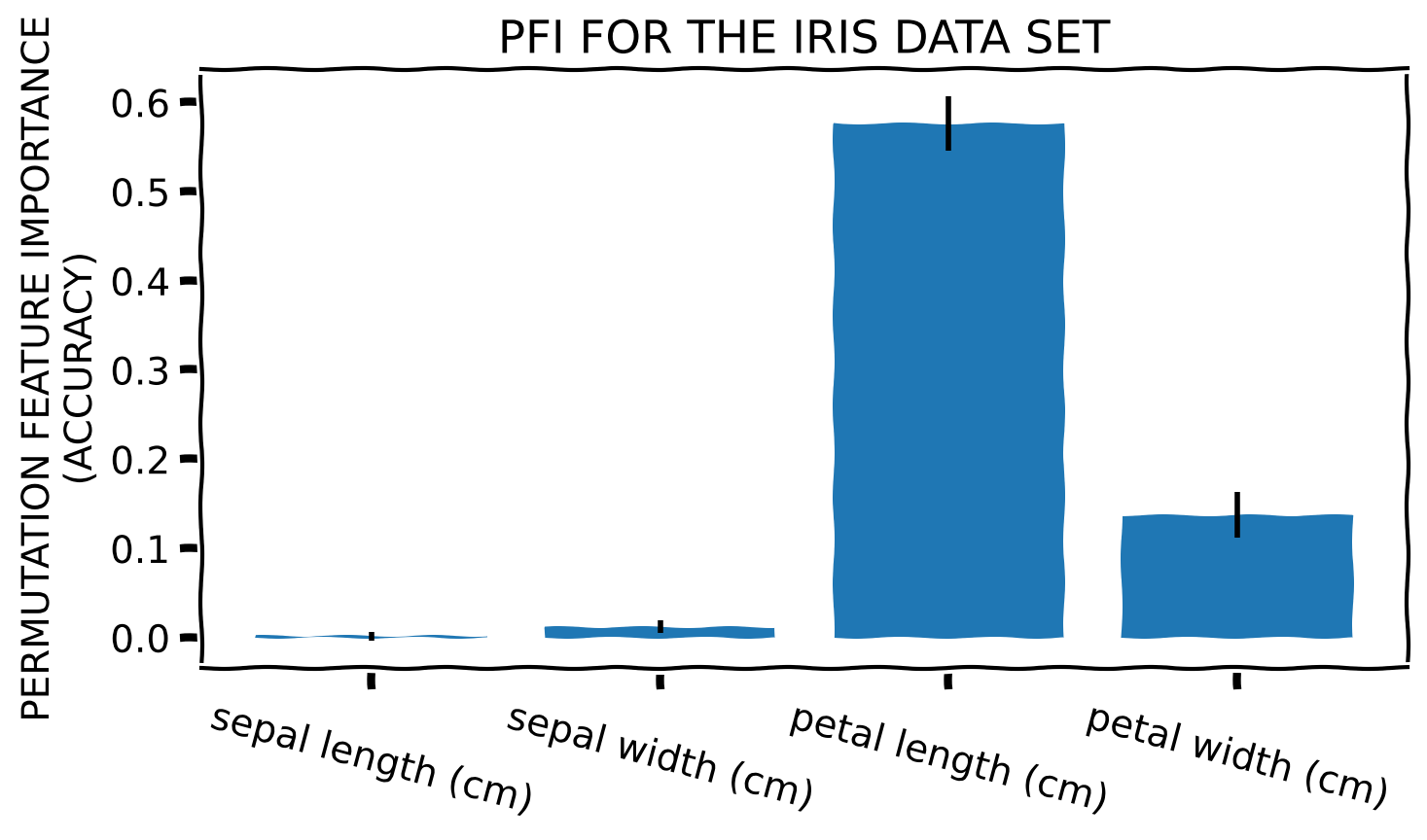
Method Properties
| Property | Permutation Feature Importance |
|---|---|
| relation | post-hoc |
| compatibility | model-agnostic |
| modelling | regression, crisp and probabilistic classification |
| scope | global (per data set; generalises to cohort) |
| target | model (set of predictions) |
Method Properties
| Property | Permutation Feature Importance |
|---|---|
| data | tabular |
| features | numerical and categorical |
| explanation | feature importance (numerical reporting, visualisation) |
| caveats | feature correlation, model’s goodness of fit, access to data labels, robustness (randomness of permutation) |
(Algorithmic) Building Blocks
Computing PFI
Input
- Optionally, select a subset of features to explain
- Select a predictive performance metric to assess degradation of utility when permuting the features; it has to be compatible with the type of the modelling problem (crisp classification, probabilistic classification or regression)
- Select a collection of instances to generate the explanation
Computing PFI
Parameters
- Define the number of rounds during which feature values will be permuted and the drop in performance recorded
- Specify the permutation protocol
Permutation Protocol
PFI is limited to tabular data primarily due to he nature of the employed feature permutation protocol. In theory, this limitation can be overcome and PFI expanded to other data types if a meaningful permutation strategy – or a suitable proxy – can be designed.
Computing PFI
Procedure
Calculate predictive performance of the explained model on the provided data using the designated metric
For each feature selected to be explained, permute its values
- Evaluate performance of the explained model on the altered data set
- Quantify the change in predictive performance
Repeat the process the number of times specified by the user to improve the reliability of the importance estimate
Theoretical Underpinning
Formulation
\[ I_{\textit{PFI}}^{j} = \frac{1}{N} \sum_{i = 1}^N \frac{\overbrace{\mathcal{L}(f(X^{(j)}), Y)}^{\text{permute feature j}}}{\mathcal{L}(f(X), Y)} \]
Performance Change Quantification
- Difference \[ \mathcal{L}(f(X^{(j)}), Y) - \mathcal{L}(f(X), Y) \]
- Quotient \[ \frac{\mathcal{L}(f(X^{(j)}), Y)}{\mathcal{L}(f(X), Y)} \]
- Percent change \[ 100 \times \frac{\mathcal{L}(f(X^{(j)}), Y) - \mathcal{L}(f(X), Y)}{\mathcal{L}(f(X), Y)} \]
Variants
Selecting Data
- PFI needs a representative sample of data to output a meaningful explanation
- The meaning of PFI is decided by the sample of data used for its generation
Selecting Data
Some choices are
- Training Data – instances used to train the explained model
- Validation Data – instances used to evaluate the predictive performance the explained model; also employed for hyperparameter tuning
- Test Data – instances used to estimate the final, unbiased predictive performance of the explained model
- Explainability Data – a separate pool of instances reserved for explaining the behaviour of the model
PFI Based on Training Data
This explanation communicates how the model relies on data features during training, but not necessarily how the features influence predictions of unseen instances. The model may learn a relationship between a feature and the target variable that is due to a quirk of the training data – a random pattern present only in the training data sample that, e.g., due to overfitting, can add some extra performance just for predicting the training data.
PFI Based on Training Data
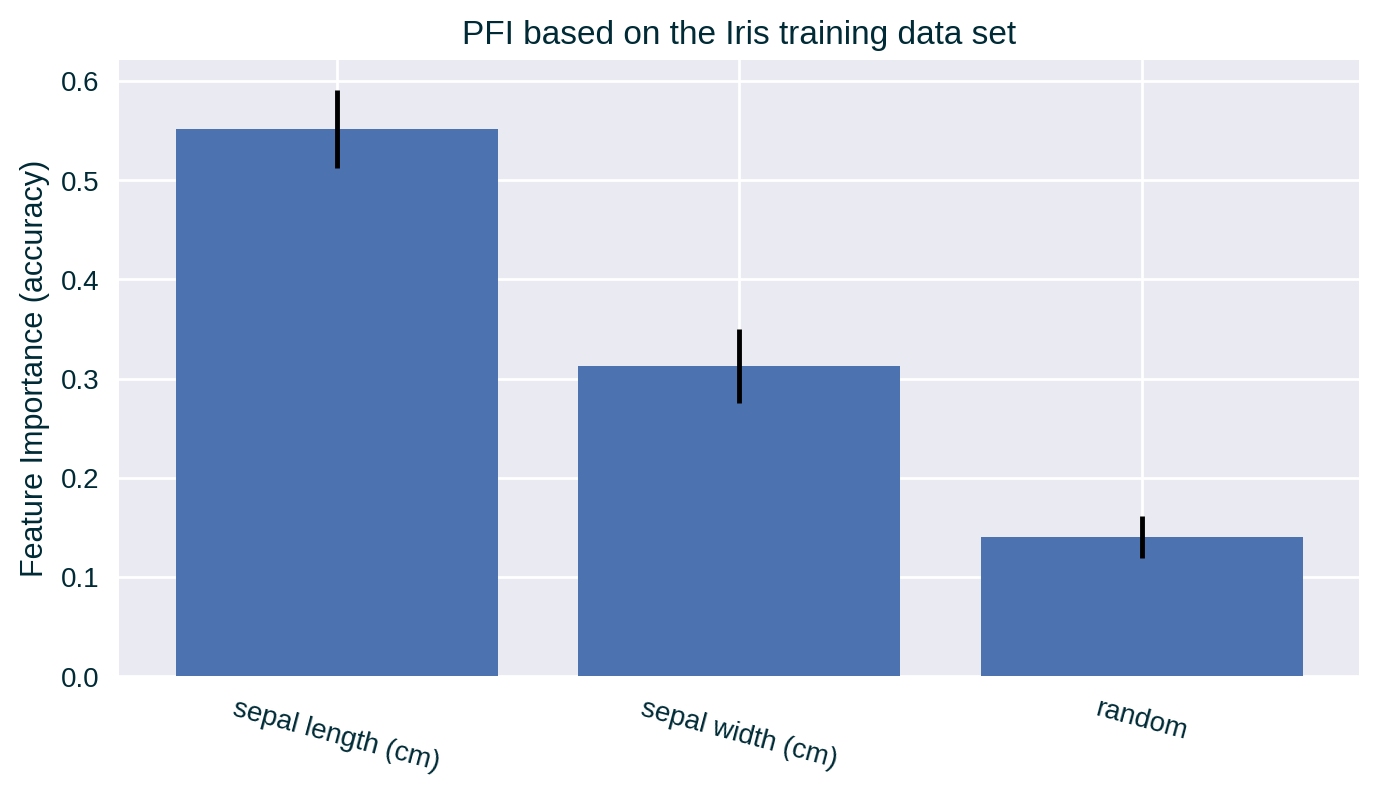
PFI Based on Test Data
The spurious correlations between data features and the target found uniquely in the training data or extracted due to overfitting are absent in the test data (previously unseen by the model). This allows PFI to communicate how useful each feature is for predicting the target, or whether some of the data feature contributed to overfitting.
PFI Based on Test Data
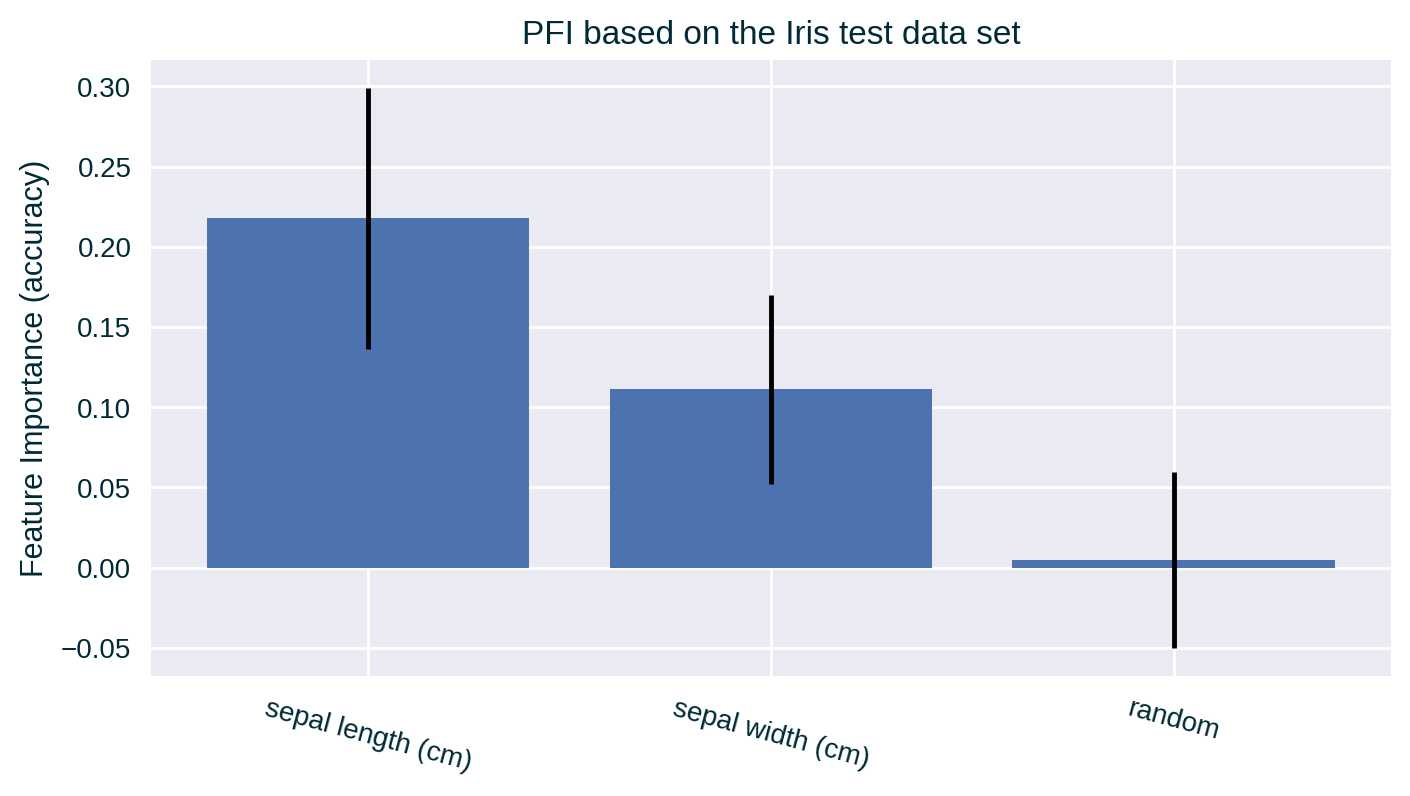
Other Measures of Feature Importance
PD-based Feature Importance
We can measure feature importance with alternative techniques such as Partial Dependence-based feature importance. This metric may not pick up the random feature’s lack of predictive power since PD generates unrealistic instances that could follow the spurious pattern found in the training data.
Other Measures of Feature Importance
PD-based Feature Importance
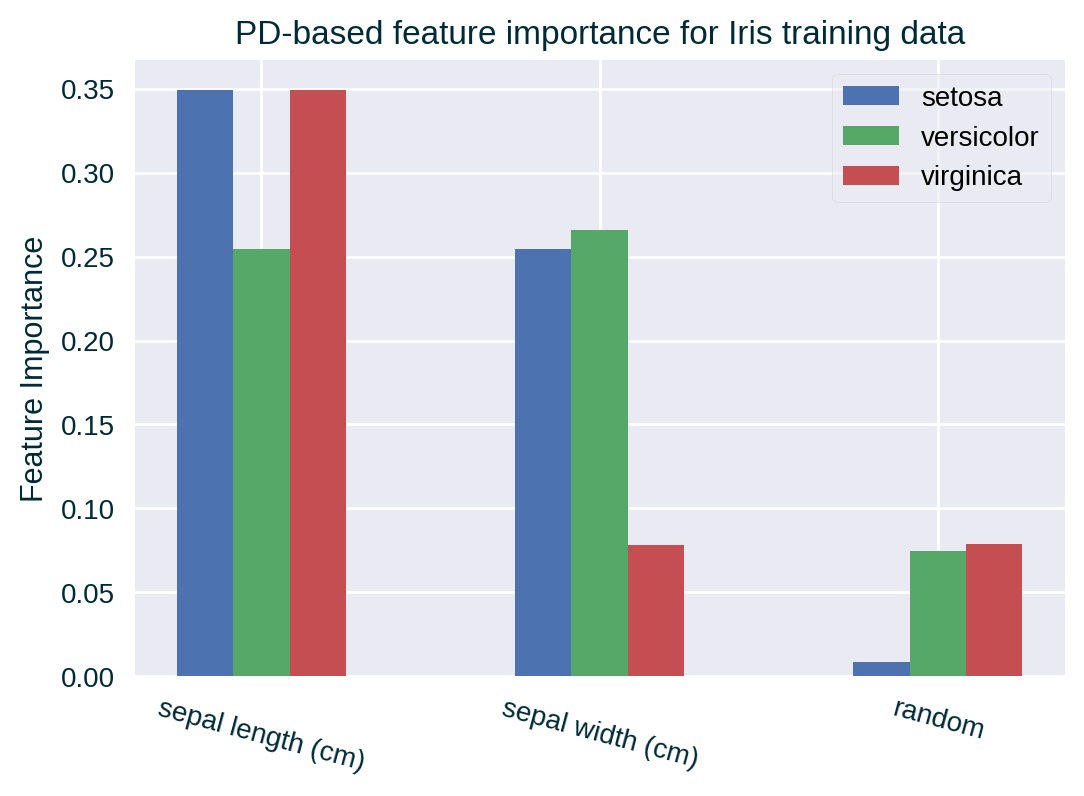
Other Measures of Feature Importance
PD-based Feature Importance
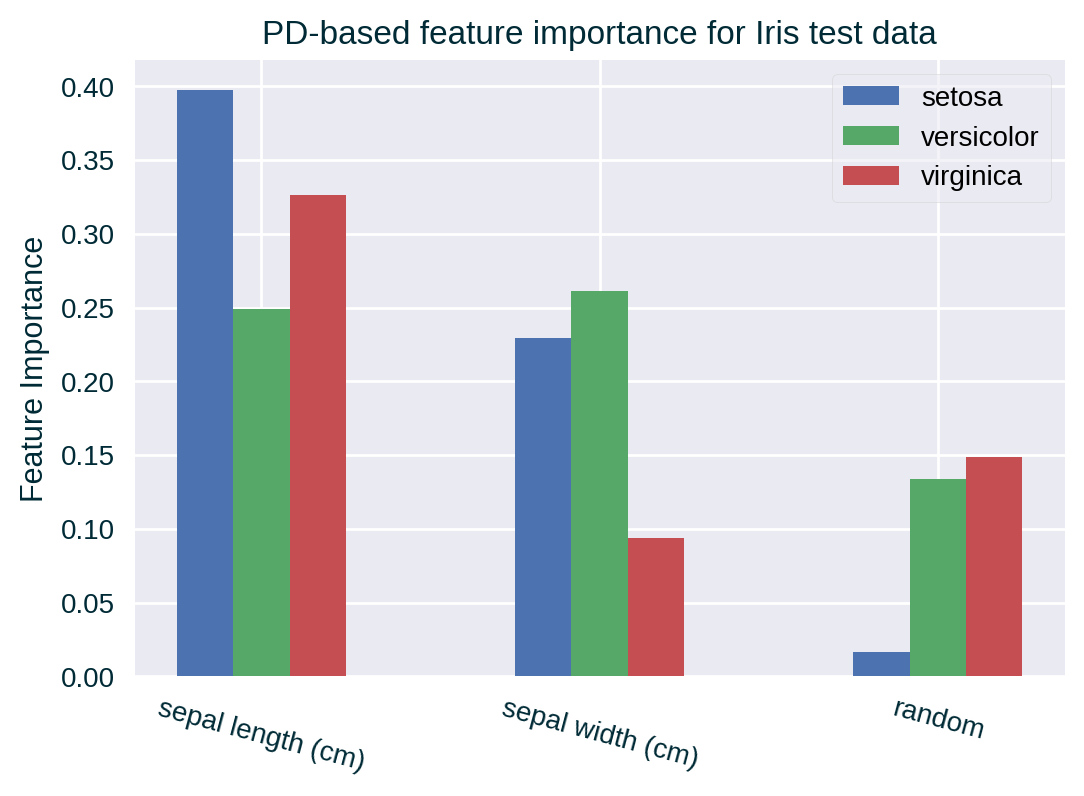
Other Measures of Feature Importance
PD-based Feature Importance
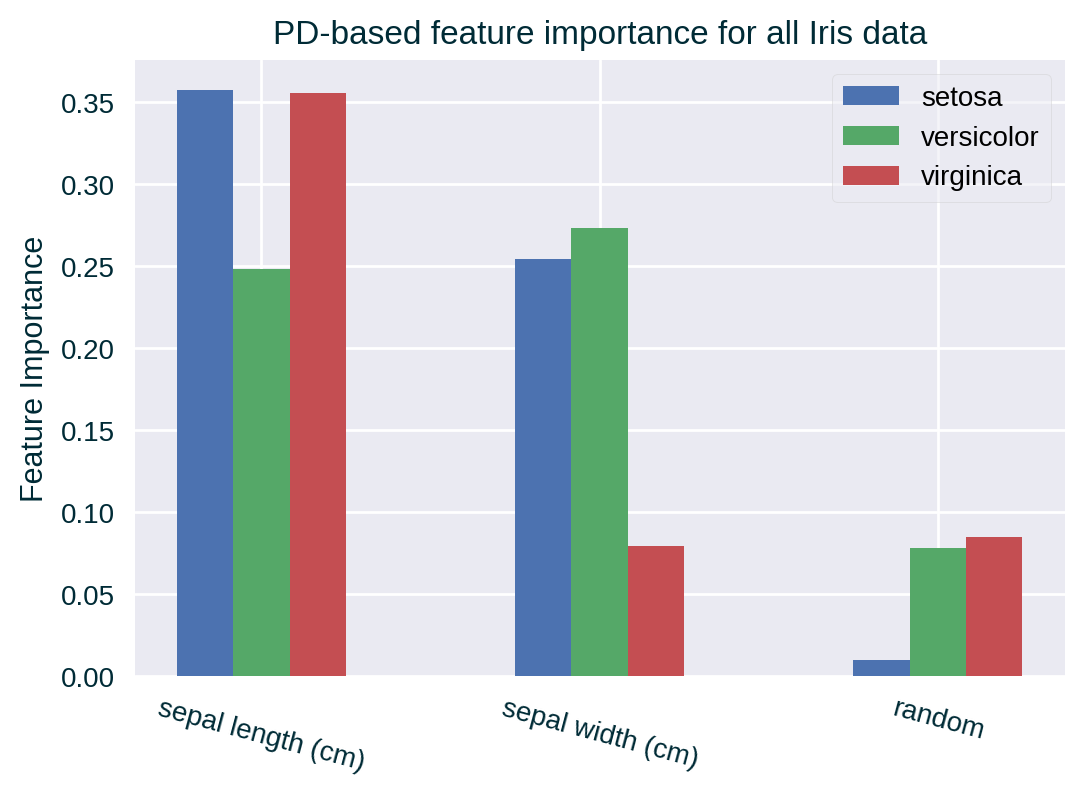
Other Measures of Feature Importance
Tree-based Feature Importance
Since the underlying predictive model (the one being explained) is a Decision Tree, we have access to its native estimate of feature importance. It conveys the overall decrease in the chosen impurity metric for all splits based on a given feature, by default calculated over the training data.
Estimate Based on Alternative Data Set
Consider implementing the same feature importance calculation protocol for other data sets, e.g., the test data.
Other Measures of Feature Importance
Tree-based Feature Importance
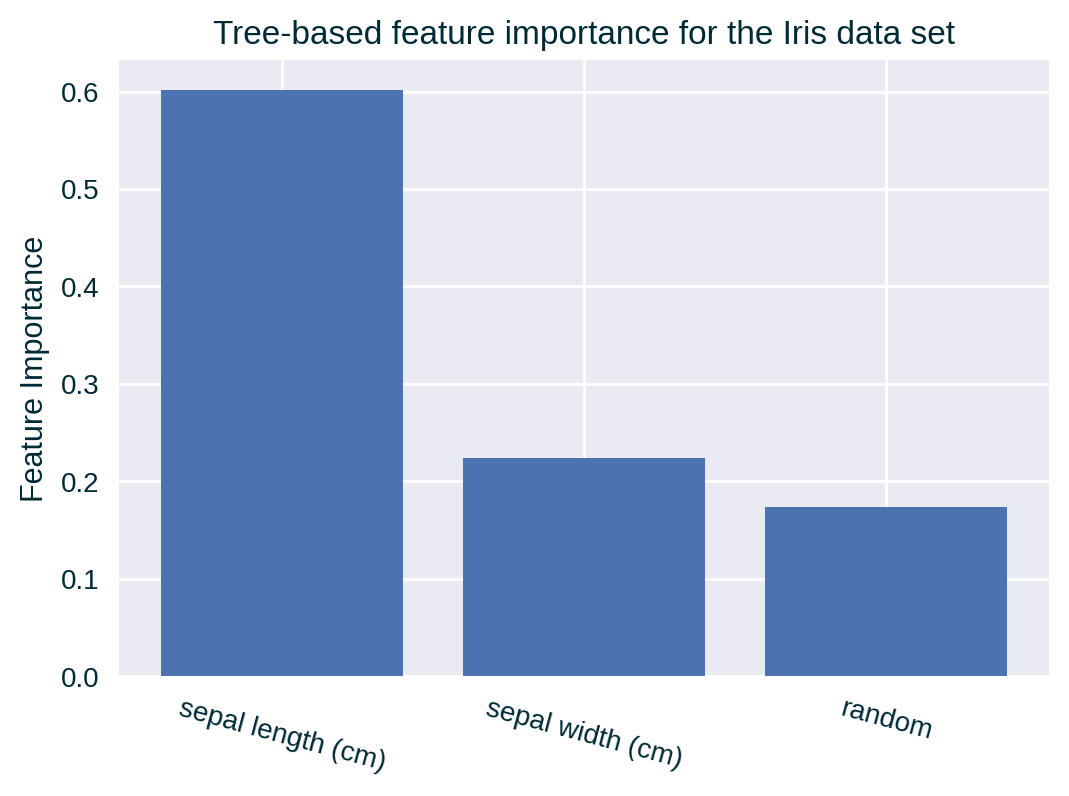
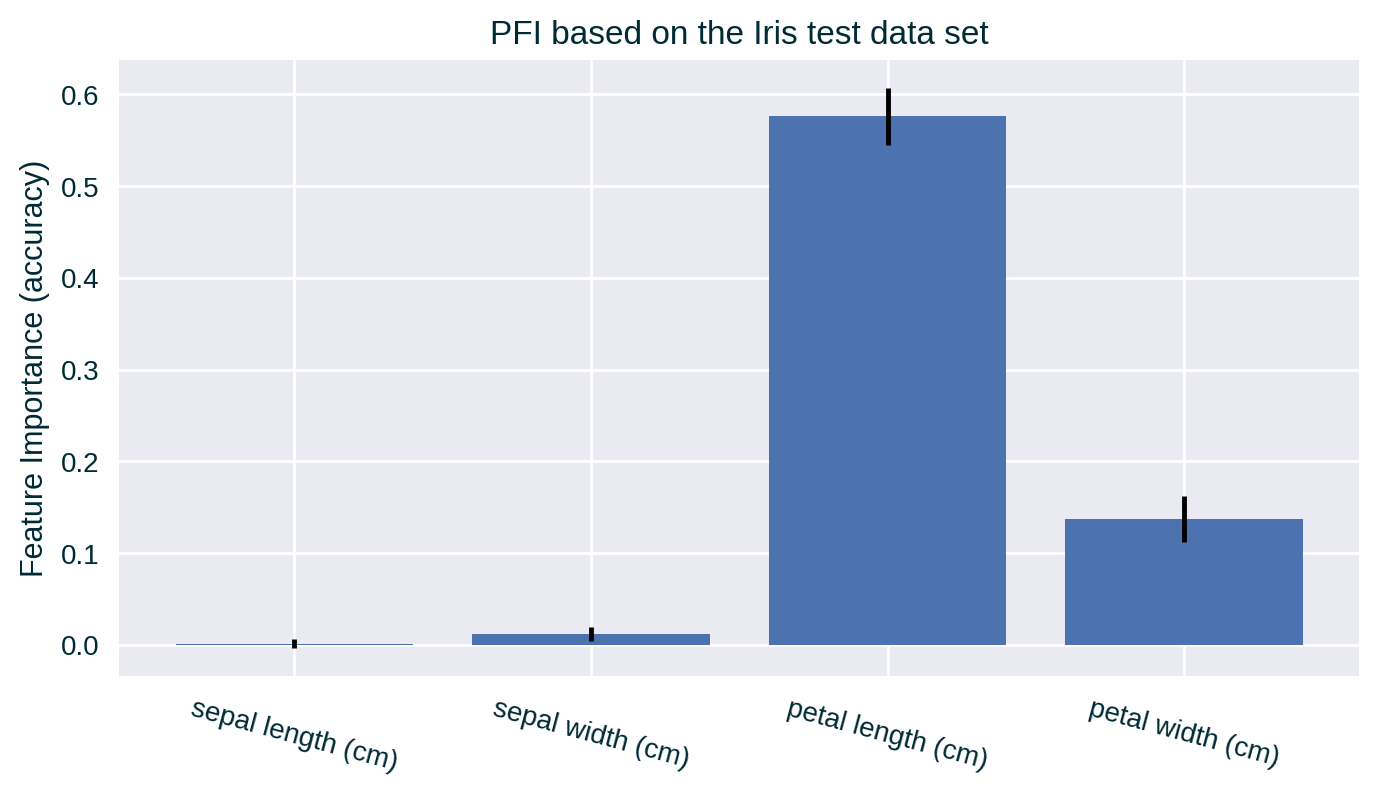
Examples
PFI – Bar Plot
PFI – Box Plot
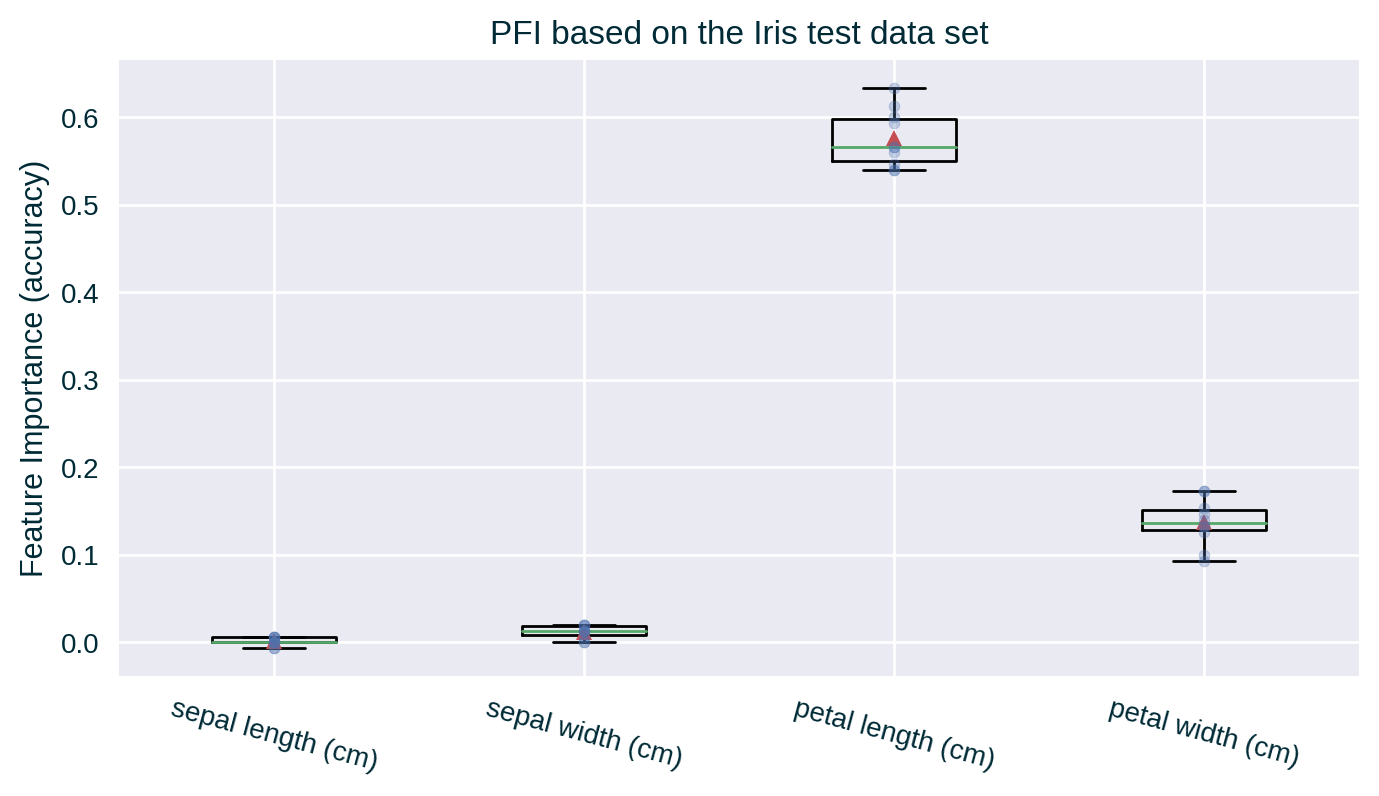
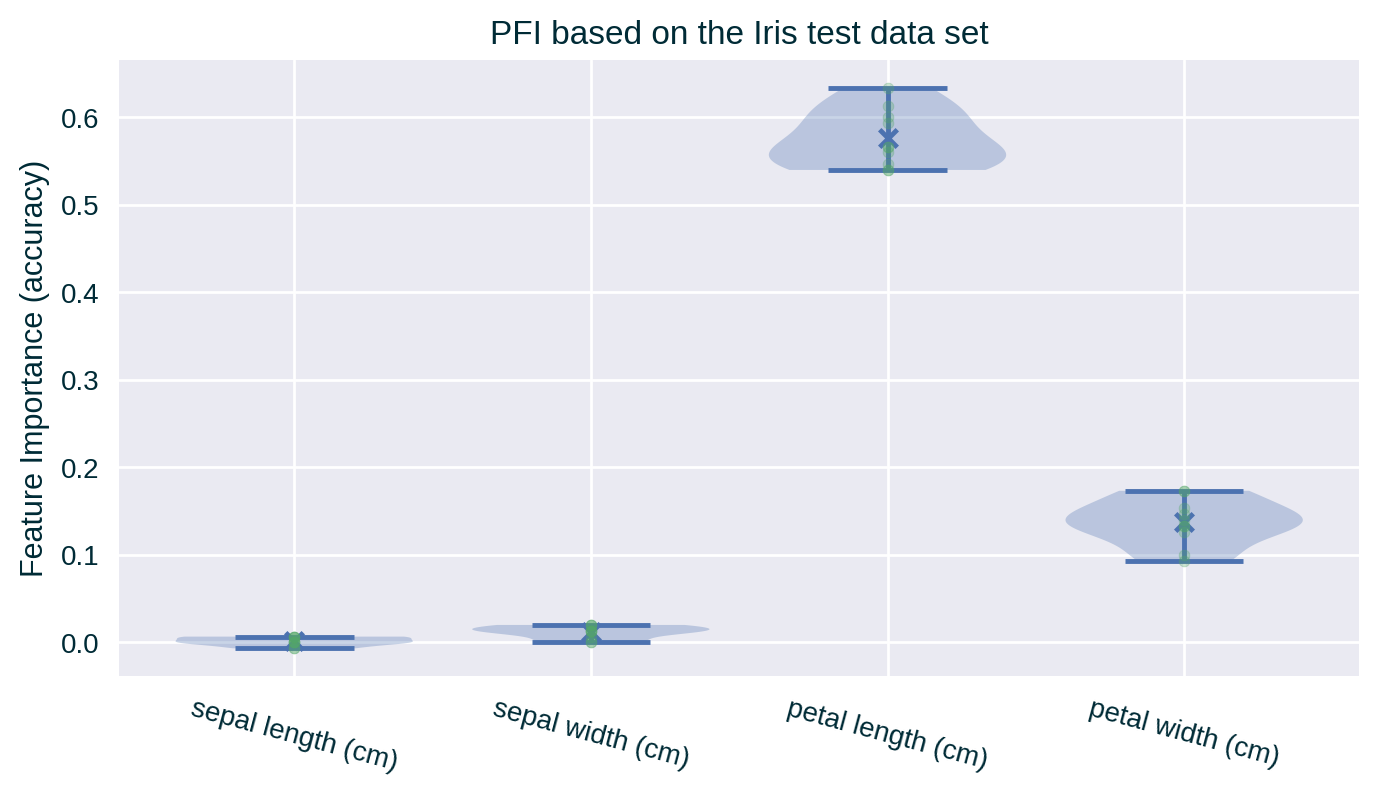
PFI – Violin Plot
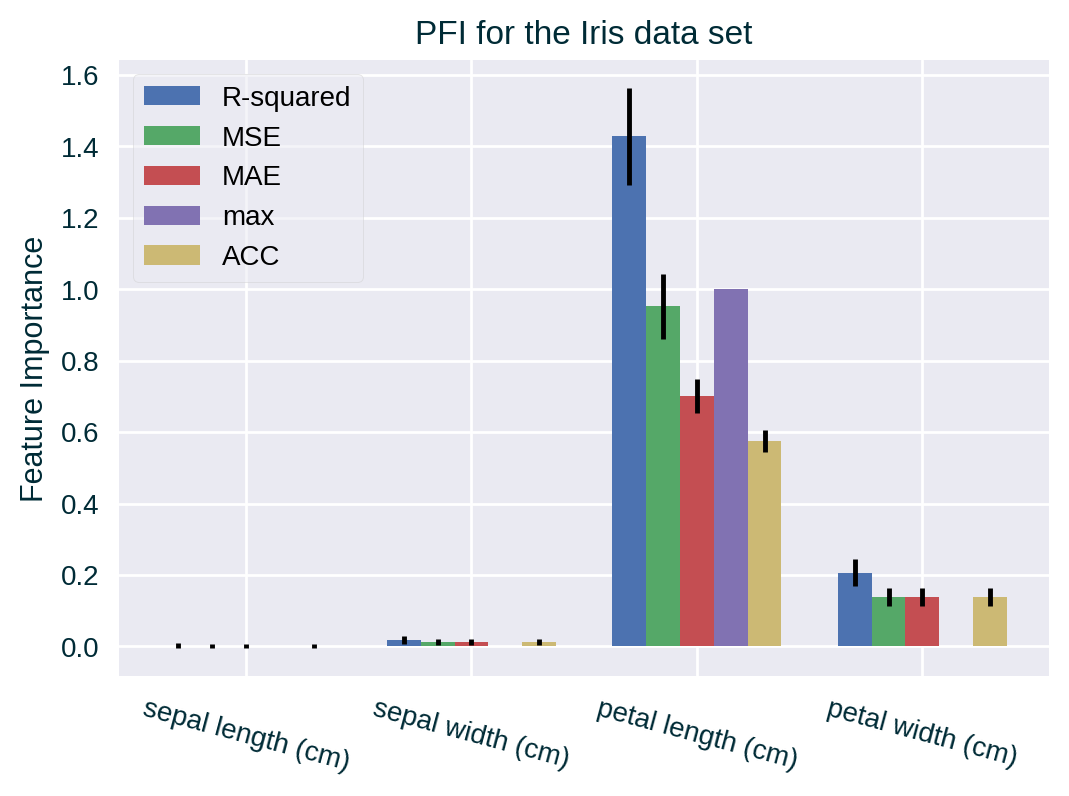
PFI for Different Metrics
Case Studies & Gotchas!
Out-of-distribution (Impossible) Instances
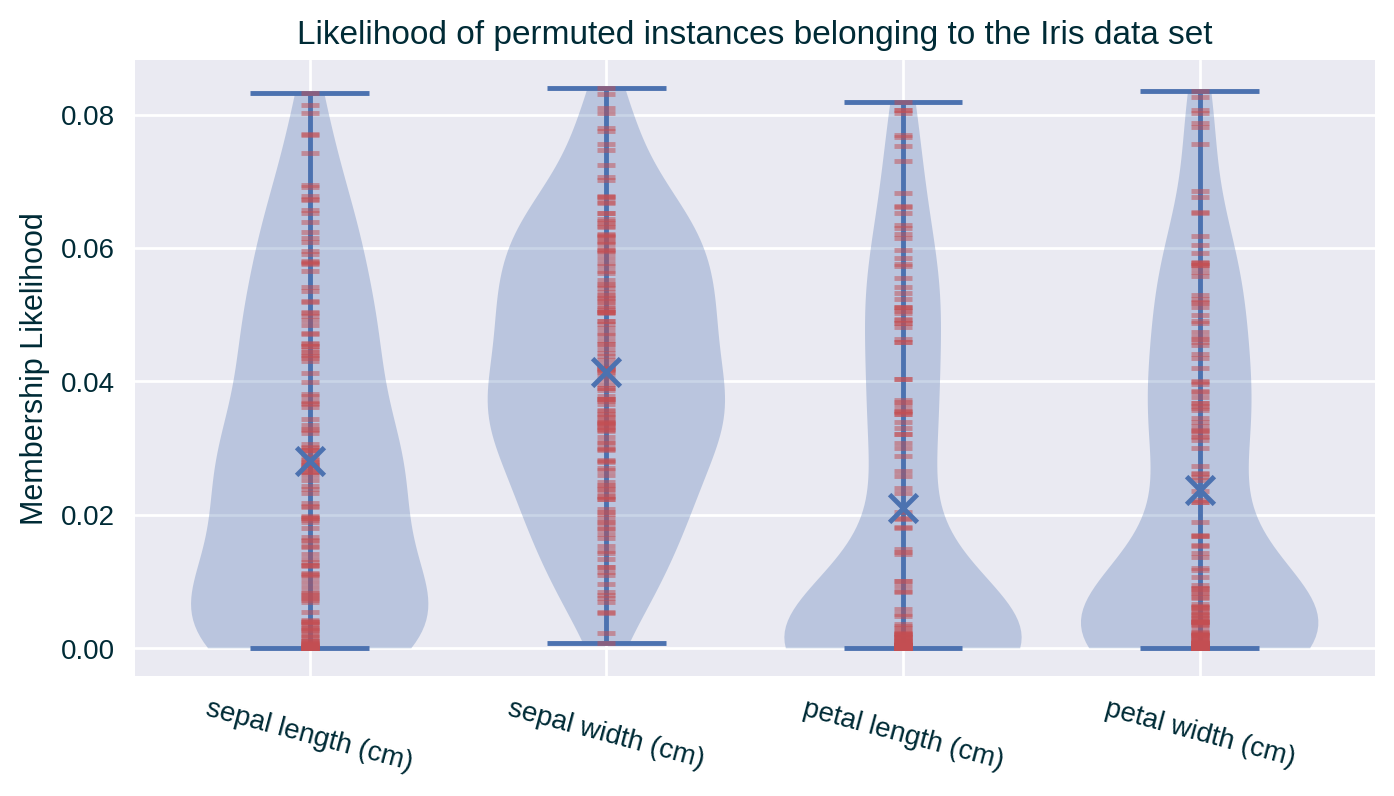
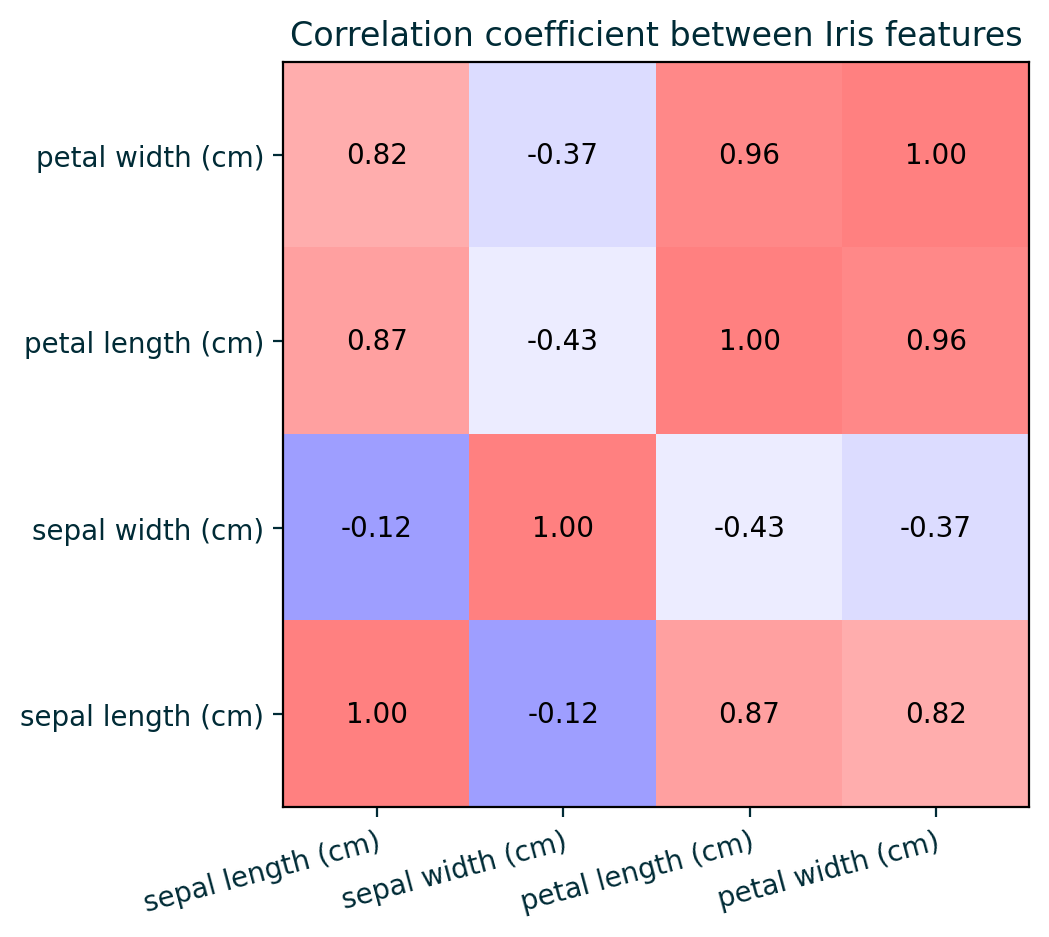
Feature Correlation
Properties
Pros
- Easy to generate and interpret
- All of the features can be explained at the same time
- Computationally efficient in comparison to a brute-force approach such as leave-one-out and retrain (which also has a different interpretation)
- Accounts for the importance of the explained feature and all of its interactions with other features (which can also be considered a disadvantage)
Cons
- Requires access to ground truth (i.e., data and their labels)
- Influenced by randomness of permuting feature values (somewhat abated by repeating the calculation mulitple times at the expense of extra compute)
- Relies on the underlying model’s goodness of fit since it is based on (the drop in) a predictive perfromance metric (in contrast to a more generic change in predictive behaviour – think predictive robustness)
Cons
Assumes feature independence, which is often unreasonable
May not reflect the true feature importance since it is based upon the predictive ability of the model for unrealistic instances
In presence of feature interaction, the importance – that one of the attributes would accumulate if alone – may be distributed across all of them in an arbitrary fashion (pushing them down the order of importance)
Since it accounts for indiviudal and interaction importance, the latter component is accounted for multiple times, making the sum of the scores inconsistent with (larger than) the drop in predictive performance (for the difference-based variant)
Caveats
PFI is parameterised by:
- data set
- predictive performance metric
- number of repetitions
Generating PFI may be computationally expensive for large sets of data and high number of repetitions
Computational complexity: \(\mathcal{O} \left( n \times d \right)\), where
- \(n\) is the number of instances in the designated data set and
- \(d\) is the number of permutation repetitions
Further Considerations
Related Techniques
Built-in Feature Importance
Many data-driven predictive models come equipped with some variant of feature importance. This includes Decision Trees and Linear Models among many others.
Related Techniques
Partial Dependence-based (PD) Feature Importance
Partial Dependence captures the average response of a predictive model for a collection of instances when varying one of their features (Friedman 2001). By assessing flatness of these curves we can derive a feature importance measurement (Greenwell, Boehmke, and McCarthy 2018).
Related Techniques
SHapley Additive exPlanations-based (SHAP) Feature Importance
SHapley Additive exPlanations explains a prediction of a selected instance by using Shapley values to computing the contribution of each individual feature to this outcome (Lundberg and Lee 2017). It comes with various aggregation mechanisms that allow to transform individual explanations into global, model-based insights such as feature importance.
Related Techniques
Local Interpretable Model-agnostic Explanations-based (LIME) Feature Importance
Local Interpretable Model-agnostic Explanations is a surrogate explainer that fits a linear model to data (expressed in an interpretable representaion) sampled in the neighbourhood of an instance selected to be explained (Ribeiro, Singh, and Guestrin 2016). This local, inherently transparent model simplifies the black-box decision boundary in the selected sub-space, making it human-comprehensible. Given that these explanations are based on coefficients of the surrogate linear model, they can also be interpreted as (interpretable) feature importance.
Implementations
| Python | R |
|---|---|
scikit-learn (>=0.24.0) |
iml |
| alibi | vip |
| Skater | DALEX |
| rfpimp |