Surrogate Explainers

(bLIMEy)

Kacper Sokol

Topics

• Method Overview
• (Algorithmic) Building Blocks
• Theoretical Underpinning
• Variants
• Evaluation
• Examples
• Case Studies & Gotchas!
• Properties
• Further Considerations

Method Overview

Explanation Synopsis

Surrogate explainers construct an inherently interpretable model in a desired – local, cohort or global – subspace to approximate a more complex, black-box decision boundary (Sokol et al. 2019).

Explanation Synopsis    

By using different surrogate models we can generate a wide array of explanation types; e.g., counterfactuals with decision trees (van der Waa et al. 2018; Sokol and Flach 2020) and feature influence with linear classifiers (Ribeiro, Singh, and Guestrin 2016).

Explanation Synopsis    

Explanation Synopsis    

Explanation Synopsis    

Interpretation of the Toy Example

• The intuition communicated by the toy example may be misleading when dealing with real-life surrogates, which often use an interpretable representation
• (Interpretable representations transform raw features into human-intelligible concepts)
• In this case surrogates do not directly approximate the behaviour of the underlying black box
• Instead, they capture its behaviour through the prism of concepts encoded by the interpretable representation

Toy Example – Tabular Data (LIME-like Linear Surrogate)

Toy Example – Image Data (LIME-like Linear Surrogate)

Toy Example – Text Data (LIME-like Linear Surrogate)

\(x^\star_0\): This

\(x^\star_1\): sentence

\(x^\star_2\): has

\(x^\star_3\): a

\(x^\star_4\): positive

\(x^\star_5\): sentiment

\(x^\star_6\): ,

\(x^\star_7\): maybe

\(x^\star_8\): .

Method Properties

Property	Surrogate Explainers
relation	post-hoc
compatibility	model-agnostic ([semi-]supervised)
modelling	regression, crisp and probabilistic classification
scope	local, cohort, global
target	prediction, sub-space, model

• Post-hoc – can be retrofitted into pre-existing predictors
• Model-agnostic – work with any black box

Method Properties    

Property	Surrogate Explainers
data	text, image, tabular
features	numerical and categorical (tabular data)
explanation	type depends on the surrogate model
caveats	random sampling, explanation faithfulness & fidelity

• Data-universal – work with image, tabular and text data because of interpretable data representations

(Algorithmic) Building Blocks

Surrogate Components

Interpretable Representation

Data Sampling

Explanation Generation

Surrogate Components: Interpretable Representation    

If desired, data are transformed from their original domain into a human-intelligible representation, which is used to communicate the explanations. This step is required for image and text data, but optional – albeit helpful – for tabular data.

Surrogate Components: Interpretable Representation        

Interpretable representations tend to be binary spaces encoding presence (fact denoted by \(1\)) or absence (foil denoted by \(0\)) of certain human-understandable concepts generated for a data point selected to be expalined.

Operationalisation of Interpretable Representations

Specifying the foil of an interpretable representation – i.e., the operation linked to switching off a component of the IR by setting its binary value to \(0\) – may not always be straightforward, practical or even (computationally) feasible in certain domains, requiring a problem-specific information removal proxy.

Surrogate Components: Interpretable Representation        

Tabular    

Discretisation of continuous features followed by binarisation.

Image    

Super-pixel segmentation.

Text    

Tokenisation such as bag-of-words representation.

Surrogate Components: Interpretable Representation        

Text    

\(x^\star_0\): This

\(x^\star_1\): sentence

\(x^\star_2\): has

\(x^\star_3\): a

\(x^\star_4\): positive

\(x^\star_5\): sentiment

\(x^\star_6\): ,

\(x^\star_7\): maybe

\(x^\star_8\): .

\[ x^\star = [1, 1, 1, 1, 1, 1, 1, 1, 1] \]

Surrogate Components: Interpretable Representation        

Text        

\[ x^\star = [1, 0, 0, 1, 0, 0, 1, 0, 1] \]

\(x^\star_0\): This

\(x^\star_1\):  

\(x^\star_2\):  

\(x^\star_3\): a

\(x^\star_4\):  

\(x^\star_5\):  

\(x^\star_6\): ,

\(x^\star_7\):  

\(x^\star_8\): .

Surrogate Components: Interpretable Representation        

Text        

This

\(x^\star_0\): sentence

has

a

\(x^\star_1\): positive

\(x^\star_1\): sentiment

,

\(x^\star_2\): maybe

.

\[ x^\star = [1, 1, 1] \]

Surrogate Components: Interpretable Representation        

Image    

\[ x^\star = [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1] \]

Surrogate Components: Interpretable Representation        

Image        

\[ x^\star = [1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1] \]

Surrogate Components: Interpretable Representation        

Image        

\[ x^\star = [1, 1, 1, 1] \]

Surrogate Components: Interpretable Representation        

Image        

\[ x^\star = [1, 1, 1] \]

Surrogate Components: Interpretable Representation        

Tabular    

\[ x = [1.3, 0.2] \]

\[ x^\prime = [0, 0] \]

Surrogate Components: Interpretable Representation        

Tabular        

\[ x^\star = [1, 1] \]

Surrogate Components: Interpretable Representation        

Tabular        

\[ x^\star = [1, 0] \]

Surrogate Components: Interpretable Representation        

Tabular        

\[ x^\star = [1, 0] \;\;\;\; \longrightarrow \;\;\;\; x = [?, ?] \]

Surrogate Components: Data Sampling    

Data sampling allows to capture the behaviour of a predictive model in a desired subspace. To this end, a data sample is generated and predicted by the explained model, offering a granular insight into its decision surface.

Surrogate Components: Data Sampling        

Original Domain

• Tabular data

Interpretable Representation

• Tabular data (implicitly global)
• Image data (implicitly local)
• Text data (implicitly local)

• With the interpretable representation, a complete sample can be generated to improve quality of the surrogate

Surrogate Components: Data Sampling        

Tabular    

Surrogate Components: Data Sampling        

Tabular        

Surrogate Components: Explanation Generation    

Explanatory insights are extracted from an inherently transparent model fitted to the sampled data (in interpretable representation), using their black-box predictions as the target.

Surrogate Components: Explanation Generation        

Additional processing steps can be applied to tune and tweak the surrogate model, hence the explanation. For example, the sample can be weighted based on its proximity to the explained instance when dealing with local explanations; and a feature selection procedure may be used to introduce sparsity, therefore improve accessibility and comprehensibility of explanatory insights.

Surrogate Components: Explanation Generation        

Sample Weighting

Data Domain

• Original domain
• (Intermediate) discrete domain (tabular data only)
• Binary interpretable representation

Distance Metric

• Hamming:
  \(L(a, b) = \frac{1}{N} \sum_{i = 1}^{N} \mathbb{1} (a_i \neq b_i)\)
• Euclidean:
  \(L(a, b) = \sqrt{\sum_{i = 1}^{N} (b_i - a_i)^2}\)
• Cosine:
  \(L(a, b) = \frac{a \cdot b}{ \sqrt{a \cdot a} \sqrt{b \cdot b}}\)

Kernel

• Exponential:
  \(k(d) = \sqrt{exp\left(-\frac{d^2}{w^2}\right)}\)

Surrogate Components: Explanation Generation        

Sample Weighting    

Surrogate Components: Explanation Generation        

Sample Weighting    

Surrogate Components: Explanation Generation        

Target Type

Crisp Classification

• Explicit one-vs-rest:
  \(A\) and \(\neg A\)

Probabilistic Classification

• Implicit one-vs-rest:
  \(\mathbb{P}(A)\) and \(1 - \mathbb{P}(A) = \mathbb{P}(\neg A)\)

Regression

• Numerical output:
  \(f(x)\)

Surrogate Components: Explanation Generation        

Modelling Multiple Classes

Single Target

Independent surrogate models explaining one class at a time:

• \(\mathbb{P}(A)\) and \(\mathbb{P}(\neg A)\)
• \(\mathbb{P}(B)\) and \(\mathbb{P}(\neg B)\)
• etc.

Multiple Targets

A single model explaining a selected subset of classes:

• \(\mathbb{P}(A)\)
• \(\mathbb{P}(B)\)
• \(\mathbb{P}(C)\)
• \(\mathbb{P}\left(\neg (A \lor B \lor C)\right)\)

• This is especially important for probabilistic models
• Consider two examples:
  • \(\mathbb{P}(A) = 0.9\), \(\mathbb{P}(B) = 0.05\), \(\mathbb{P}(C) = 0.05\)
  • \(\mathbb{P}(A) = 0.6\), \(\mathbb{P}(B) = 0.3\), \(\mathbb{P}(C) = 0.1\)

Surrogate Components: Explanation Generation        

Surrogate Model Type

• Lienar
• Tree-based
• Rule-based
• etc.

Computing Surrogates

Computing Surrogates    

Input

1. Select an instance to be explained (local surrogate)

2. Select the explanation target

   • crisp classifiers → one-vs-rest or a subset of classes-vs-rest
   • probabilistic classifiers → (probabilities of) one or multiple classes
   • regressors → numerical values

Computing Surrogates    

Parameters

1. Define the interpretable representation
   • text → pre-processing and tokenisation
   • image → occlusion proxy, e.g., segmentation granularity and occlusion colour
   • tabular → discretisation of numerical features and grouping of categorical attributes

Computing Surrogates    

Parameters

2. Specify sampling strategy
   • original domain (tabular data) → number of instances and sampling objective (scope and target)
   • transformed domain (all data domains) → completeness of the sample
3. Sample weighting → data domain, distance metric, kernel type
4. Feature selection (tabular data) – feature selection strategy
5. Type of the surrogate model and its parameterisation

Computing Surrogates    

Procedure

1. Transform the explained instance into the interpretable representation
2. Sample data around the explained instance with a given scope
3. Predict the sampled data using the black box (transform into the original representation if sampled in the interpretable domain)

Computing Surrogates    

Procedure    

4. Calculate similarities between the explained instance and sampled data by kernelising distances
5. Optionally, reduce dimensionality of the interpretable domain
6. Fit a surrogate model to the (subset of) interpretable feature and black-box predictions of the desired target(s)
7. Extract the desired explanation from the surrogate model

Theoretical Underpinning

\[ \def\IR{\mathit{IR}} \def\argmin{\mathop{\operatorname{arg\,min}}\limits} \def\argmax{\mathop{\operatorname{arg\,max}}\limits} \]

Formulation: Optimisation Objective    

\[ \mathcal{O}(\mathcal{G}; \; f) = \argmin_{g \in \mathcal{G}} \overbrace{\Omega(g)}^{\text{complexity}} \; + \;\;\; \overbrace{\mathcal{L}(f, g)}^{\text{fidelity loss}} \]

Formulation: Complexity    

\[ \Omega(g) = \frac{\sum_{\theta \in \Theta_g} {\Large\mathbb{1}} \left(\theta\right)}{|\Theta_g|} \]

\[ \Omega(g; \; d) = \frac{\text{depth}(g)}{d} \;\;\;\;\text{or}\;\;\;\; \Omega(g; \; d) = \frac{\text{width}(g)}{2^d} \]

Formulation: Numerical Fidelity (One Class)    

\[ \mathcal{L}(f, g ; \; \mathring{x}, X^\prime, \mathring{c}) = \sum_{x^\prime \in X^\prime} \; \underbrace{\omega\left( \IR(\mathring{x}), x^\prime \right)}_{\text{weighting factor}} \; \times \; \underbrace{\left(f_\mathring{c}\left(\IR^{-1}(x^\prime)\right) - g(x^\prime)\right)^{2}}_{\text{individual loss}} \]

\[ \omega\left(\IR(\mathring{x}), x^\prime \right) = k\left(L\left(\IR(\mathring{x}), x^\prime\right)\right) \]

\[ \omega\left( \mathring{x}, x \right) = k\left(L\left(\mathring{x}, x\right)\right) \]

Formulation: Crisp Classification Fidelity (One Class)    

\[ \mathcal{L}(f, g ; \; \mathring{x}, X^\prime, \mathring{c}) = \sum_{x^\prime \in X^\prime} \; \omega\left( \IR(\mathring{x}), x^\prime \right) \; \times \; \underline{ {\Large\mathbb{1}} \left(f_\mathring{c}\left(\IR^{-1}(x^\prime)\right), \; g(x^\prime)\right)} \]

\[ \begin{split} f_{\mathring{c}}(x) = \begin{cases} 1, & \text{if} \;\; f(x) \equiv \mathring{c}\\ 0, & \text{if} \;\; f(x) \not\equiv \mathring{c} \end{cases} \text{ .} \end{split} \]

\[ \begin{split} {\Large\mathbb{1}}\left(f_{\mathring{c}}(x), g(x^\prime)\right) = \begin{cases} 1, & \text{if} \;\; f_{\mathring{c}}(x) \equiv g(x^\prime)\\ 0, & \text{if} \;\; f_{\mathring{c}}(x) \not\equiv g(x^\prime) \end{cases} \text{ ,} \end{split} \]

Formulation: Crisp Classification Fidelity (One Class)        

\(f(x)\)	\(f_\beta(x)\)	\(g(x^\prime)\)	\({\Large\mathbb{1}}\)
\(\alpha\)	\(0\)	\(1\)	\(0\)
\(\beta\)	\(1\)	\(0\)	\(0\)
\(\gamma\)	\(0\)	\(0\)	\(1\)
\(\beta\)	\(1\)	\(1\)	\(1\)
\(\alpha\)	\(0\)	\(0\)	\(1\)

Formulation: Crisp Classification Fidelity (Multiple Class)    

\[ \mathcal{L}(f, g ; \; \mathring{x}, X^\prime, \mathring{C}) = \sum_{x^\prime \in X^\prime} %\left( \omega( \IR(\mathring{x}) , x^\prime ) \; \times \; \underline{ \frac{1}{|\mathring{C}|} \sum_{\mathring{c} \in \mathring{C}} {\Large\mathbb{1}} \left( f_\mathring{c}\left(\IR^{-1}(x^\prime)\right), \; g_\mathring{c}(x^\prime) \right) } %\right) \]

Formulation: Numerical Fidelity (Multiple Class)    

\[ \mathcal{L}(f, g ; \; \mathring{x}, X^\prime, \mathring{C}) = \sum_{x^\prime \in X^\prime} %\left( \omega( \IR(\mathring{x}) , x^\prime ) \; \times \; \underline{ \frac{1}{2} \sum_{\mathring{c} \in \mathring{C}} \left( f_\mathring{c}\left(\IR^{-1}(x^\prime)\right) - g_\mathring{c}(x^\prime) \right)^2 } %\right) \]

Variants

As many as you wish to construct.

Evaluation

Fidelity-based

Tabular Data: Interpretable Representation

Tabular Data: Sampling

Examples

One-class Linear Surrogate

One-class Linear Surrogate    

One-class Linear Surrogate    

Multi-class Tree Surrogate

Case Studies & Gotchas!

Image Data: Segmentation Size & Occlusion Colour

Image Data: Segmentation Size & Occlusion Colour    

• Note that linear model’s assumptions are broken – adjacent super-pixels are highly correlated

Image Data: Segmentation Size & Occlusion Colour    

Image Data: Segmentation Size & Occlusion Colour    

Tabular Data: Incompatibility of Binarisation and Linear Models

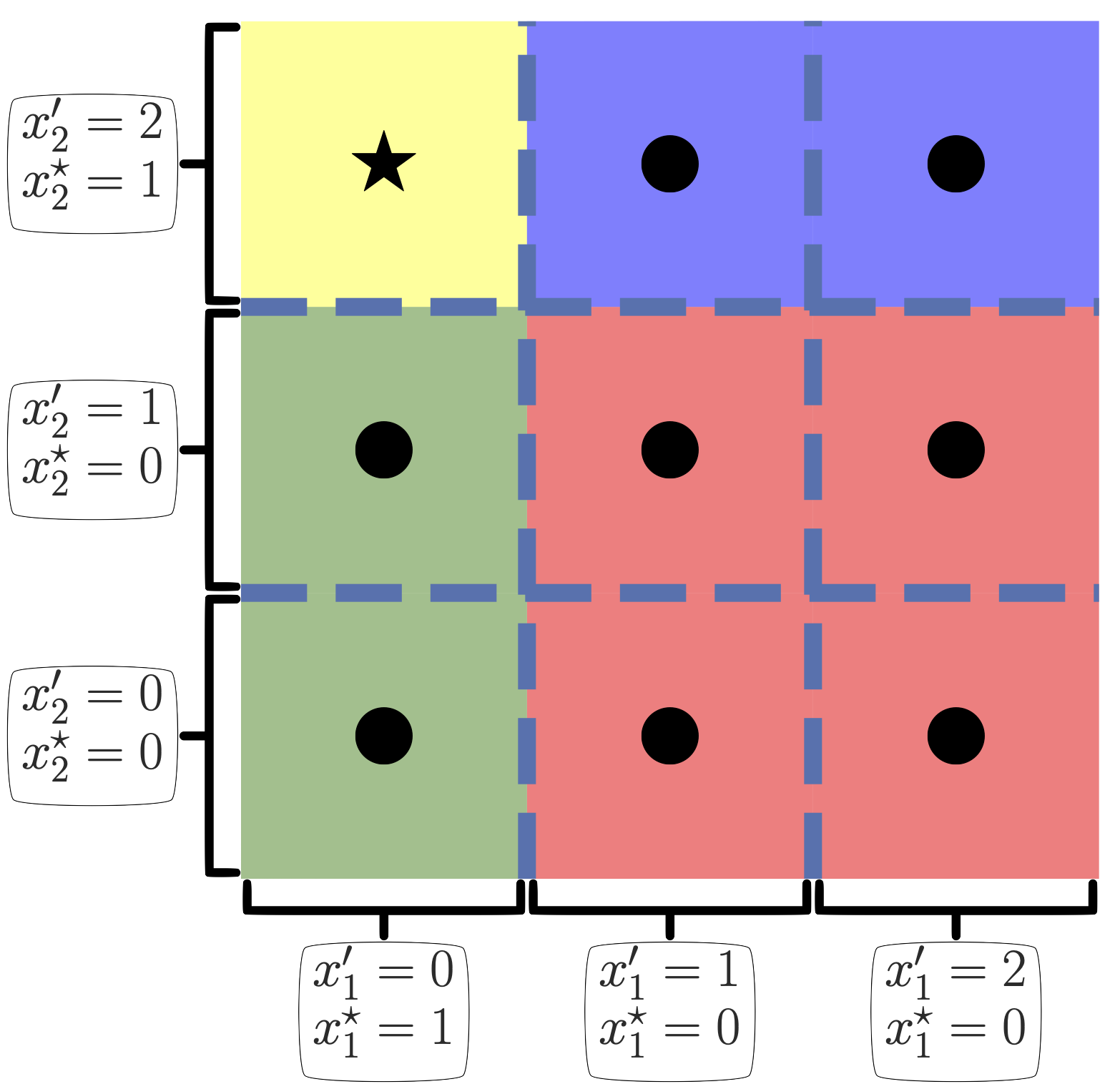
Tabular Data: Incompatibility of Binarisation and Linear Models    

Properties

Pros    

• A universal inspection mechanism for various subspaces of an arbitrary black-box algorithmic decision process
• Highly customisable
• A single explanatory procedure for image, text and tabular data
• Produces diverse explanation types depending on the utilised surrogate model
• Outputs intuitive explanations for image and text data due to the use of interpretable representations

Cons    

• Inadequate for high-stakes algorithmic decisions because of lacklustre fidelity
• Explanations may be counterintuitive and misleading for a lay audience when applied to tabular data with an interpretable representation

Caveats    

• While post-hoc, model-agnostic and data-universal, they must not be treated as a silver bullet
• Their characteristics allow a single instantiation of a surrogate explainer to be applied to diverse problems, however the quality of the resulting explanations will vary across different problems and data sets
• Building them requires an effort since each explainer should be tweaked and tuned to the problem at hand

Further Considerations

Related Techniques

• LIME (Ribeiro, Singh, and Guestrin 2016)
• LIMEtree (Sokol and Flach 2020)
• RuleFit (Friedman and Popescu 2008)

Implementations

Python	R
LIME	lime
interpret	iml
Skater
AIX360

Further Reading

• bLIMEy paper (Sokol et al. 2019)
• LIME paper (Ribeiro, Singh, and Guestrin 2016)
• LIMEtree paper (Sokol and Flach 2020)
• Interpretable Machine Learning book
• FAT Forensics how-to guide for tabular surrogates and image surrogates, and surrogates tutorial
• Tabular surrogates tutorial
• Interactive resources

Bibliography

Friedman, Jerome H, and Bogdan E Popescu. 2008. “Predictive Learning via Rule Ensembles.” The Annals of Applied Statistics, 916–54.

Ribeiro, Marco Tulio, Sameer Singh, and Carlos Guestrin. 2016. “‘Why Should I Trust You?’: Explaining the Predictions of Any Classifier.” In Proceedings of the 22^nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, August 13–17, 2016, 1135–44.

Sokol, Kacper, and Peter Flach. 2020. “LIMEtree: Consistent and Faithful Surrogate Explanations of Multiple Classes.” arXiv Preprint arXiv:2005.01427.

Sokol, Kacper, Alexander Hepburn, Raul Santos-Rodriguez, and Peter Flach. 2019. “bLIMEy: Surrogate Prediction Explanations Beyond LIME.” 2019 Workshop on Human-Centric Machine Learning (HCML 2019) at the 33^rd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, Canada.

van der Waa, Jasper, Marcel Robeer, Jurriaan van Diggelen, Matthieu Brinkhuis, and Mark Neerincx. 2018. “Contrastive Explanations with Local Foil Trees.” Workshop on Human Interpretability in Machine Learning (WHI 2018) at the 35^th International Conference on Machine Learning (ICML 2018), Stockholm, Sweden.